F5 - La lampe va-t-elle griller

Document d’accompagnement – Physique / classe de première S © CNDP
Electrodynamique – circuit électrique en courant continu
F5
La lampe va-t-elle griller ?
Dans un circuit électrique toute l’énergie électrique fournie par le générateur est, dans le même temps,
transférée aux récepteurs. Cela signifie que la puissance à laquelle se fait le transfert d’énergie électrique
du générateur aux récepteurs satisfait à la relation PG = PR.
Mais cela ne dit pas comment se fait ce transfert d’énergie entre un générateur et les récepteurs du circuit.
En particulier comment s’adaptent les tensions et les intensités. Qui en décide : le générateur, les
récepteurs ou leur association?
Interrogés sur le rôle d’un générateur dans un circuit, beaucoup d’élèves pensent que celui-ci est seul
responsable de l’importance du courant qui s’établit dans le circuit, autrement dit que le générateur fixe la
valeur de l’intensité du courant qui circule dans sa branche. Un objectif important de ce TP consiste donc
à faire prendre conscience aux élèves du rôle joué par les récepteurs sur la valeur de l’intensité du courant
qui s’établit dans la branche du générateur. Un deuxième objectif consiste à montrer qu’il est possible de
prévoir comment se fait l’adaptation des fonctionnements des récepteurs et du générateur à partir de la
connaissance de leurs caractéristiques.
Matériel nécessaire (par groupe)
- une pile 4.5 V en bon état (fém > 4.4 V).
- des lampes à incandescence (3.5V ; 1A) (4V ; 0.5A) (6V ; 0.3A) (6V ;1A) (12V ; 1W).
- une douille.
- deux contrôleurs.
- fils de connexion.
Les élèves travaillent par deux. Ils disposent sur leur table de la lampe à incandescence (3,5V ; 1A) et
d’une pile plate (4.5V) Le reste du matériel est disponible sur un chariot. Il pourront venir le prendre au fur
et à mesure de leurs besoins.
Questionnement possible
On part de la situation problème suivante. “ On désire faire fonctionner la lampe sur la pile. A votre avis la
lampe est-elle adaptée pour fonctionner normalement ; pourquoi ? Que va-t-il se passer lorsque l’on
branchera la lampe sur la pile et pourquoi ? ”
Commentaire – La lampe de 3.5V 1A est intéressante car, de par les caractéristiques indiquées sur le
culot, elle semble ne pas convenir à la pile ; de plus, son ampoule est plus grosse que les autres ce qui lui
confère apparemment un caractère inadapté. On s’attend donc à ce que les élèves répondent dans leur
majorité que la lampe est inadaptée et qu’elle risque de griller si on la branche sur la pile (argument : la
valeur 4.5V est nettement supérieure à 3,5V).
On montre alors que le montage de la lampe sur la pile fonctionne normalement : la lampe brille bien et, en
apparence, ne semble pas “ survoltée ”. Il semble qu’il y ait problème. Comment une lampe de 3,5 V
peut-elle fonctionner sur une pile de 4,5V ?
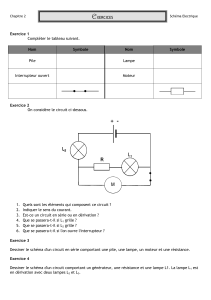
• On peut alors poser la question suivante aux élèves : “ Quel montage et quelles mesures proposez-vous
de faire pour savoir si la lampe fonctionne normalement ou pas ? ”
Commentaire – On s’attend à ce que des élèves mesurent la tension aux bornes de la pile pour en vérifier
l’état : dans ce cas ils trouveront une valeur voisine de 4,5V. Certains pourront peut-être proposer de
monter un ampèremètre dans le circuit et un voltmètre sur la lampe (ou sur la pile) selon le schéma
suivant :

Document d’accompagnement – Physique / classe de première S © CNDP
Avant d’autoriser les élèves à effectuer les mesures, on indiquera que celles-ci devront être effectuées
pendant un temps très bref (de l’ordre de quelques secondes) afin que la pile ne se décharge pas trop.
Ceci sera réalisé en vissant puis en dévissant la lampe de son culot sitôt les mesures de U et I effectuées.
Commentaire - Les élèves constatent alors que les valeurs mesurées pour U et I sont proches de 3,5V et
1A
1
. Ils constatent également que la tension remonte en quelques secondes à une valeur proche de 4.5V
lorsque la lampe est déconnectée.
Il semble que “ la pile s’adapte à la lampe ” de sorte que les valeurs de I et de U soient proches de celles
indiquées par le constructeur. En fonctionnement, la tension de la pile est inférieure à sa tension “ à vide ”.
“ Ce résultat est-il général ? ” : on suggère alors aux élèves de reprendre l’expérience avec d’autres
lampes, voire d’autres composants.
En conclusion : en fonctionnement, la tension de la pile est inférieure à sa tension “ à vide ”. Les points de
fonctionnement (U,I) de la pile dépendent du récepteur. Ainsi, la puissance à laquelle se fait le transfert de
l’énergie électrique de la pile à la lampe dépend non seulement de la pile utilisée mais encore de la lampe
qui lui est connectée. La tension aux bornes de la pile et l’intensité du courant qui la traverse s’adaptent au
récepteur qui est branché à ses bornes.
Remarque - Pour cette partie de l’étude, d’autres lampes que celles préconisées au début peuvent
convenir. On veillera simplement à ce que leurs points de fonctionnement sur une pile de 4.5V soient
suffisamment différents et que, pour les lampes dont la tension de fonctionnement est inférieure à 4.5V,
les indications portées par le constructeur sur le culot soient voisines de celles qui seront mesurées (ce qui
est loin d’être toujours le cas !). D’autres récepteurs (résistors, moteurs, etc.) peuvent également être
utilisés.
• On peut poursuivre par une question du type : “ Mais alors, comment se fait cette adaptation ? Peut-on la
prévoir pour un récepteur et une pile donnés ? ” et par le raisonnement suivant : dire que “ la pile
s’adapte ” , cela signifie que son fonctionnement est donné par un couple de valeurs (U, I). Savoir
comment se fait son adaptation aux récepteurs du circuit suppose qu’on connaisse les différents points de
fonctionnement possibles pour la pile.
Construction de l’ensemble des points de fonctionnement possibles de la pile
Il s’agit ici d’utiliser les couples de valeurs de U et de I déterminés précédemment pour construire la
caractéristique (c’est à dire l’ensemble de tous les points de fonctionnement possibles) de la pile.
Les élèves sont alors invités par le professeur à utiliser un tableur pour construire cette caractéristique. La
plupart des tableurs permettent, en général d’en déterminer l’équation. Les élèves peuvent aussi utiliser
leur calculatrice pour tracer cette caractéristique : on entre la liste des valeurs des intensités ainsi que la
liste des valeurs des tensions puis on effectue une régression linéaire.
On obtient alors l’équation de la droite représentant U en fonction de I.)
Commentaires
1
En réalité ce fonctionnement concerne la lampe et le milliampèremètre et non pas la lampe seule. La différence est cependant
généralement minime.
V
mA

Document d’accompagnement – Physique / classe de première S © CNDP
Nous donnons ci-dessous, à titre d’exemple le résultat que nous avons obtenu avec notre pile. La droite
tracée par le logiciel (ou obtenue avec une calculatrice) a pour équation : U = 4,6202 - 1,0862 x I
que l’on peut raisonnablement arrondir à : U = 4,6 - 1,1 x I
Il est alors intéressant de constater que les caractéristiques des piles distribuées dans la salle de TP ne
sont pas identiques : elles dépendent de la durée de fonctionnement de la pile avant le TP.
On peut présenter la caractéristique d'une pile en montrant la non linéarité de celle-ci si I dépasse 1.5 A
par exemple ; la non reproductibilité des résultats est flagrante si les mesures ne sont pas effectuées
suffisamment rapidement. On pourra discuter, à un niveau élémentaire, et en relation avec le cours de
chimie, du sens physique de la résistance électrique d'un conducteur, dans la pile et dans le filament de la
lampe. On signalera la complexité de phénomènes physiques, pourtant utilisés communément.
Quelle signification donner à cette équation ?
Le professeur propose de chercher à modéliser le fonctionnement d’une pile en utilisant les
connaissances déjà établies dans le cours.
Modèle d’une pile
Modélisation du fonctionnement d’une pile
On montre alors qu’il est possible d’écrire l’équation de la droite sous la forme U = b - aI et on pose aux
élèves une question du type : “ Que représentent les grandeurs a et b ? ”. Une discussion avec la classe
permet de conclure de la manière suivante :
- b représente la valeur de U lorsque I = 0 (ici 4.6V) On appelle cette grandeur force électromotrice de la
pile (fém notée E).
- a.I (ici 1,1) correspond à une tension proportionnelle à l’intensité du courant qui traverse la pile. Par sa
forme, la tension a.I s’apparente à la tension mesurée aux bornes d’une résistance a = 1,1 = r Pour
cette raison, on appelle r : résistance interne de la pile.
Le fonctionnement d’une pile peut donc être modélisé par une équation dont la forme générale est
U = E – r.I
et le schéma équivalent d’une pile est le suivant :
Pile 4,5 V
Type lampe I (A) U (V)
3,5 ; 1 0,98 3,55
4 ; 0,5 0,49 4,1
6V ; 0,3 0,22 4,34
6V ; 1A 0,81 3,75
12V ;1W 0,042 4,6
y = -1,0862x + 4,6202
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
I (A)
U (V)

Document d’accompagnement – Physique / classe de première S © CNDP
Vérification de la validité du modèle
On réalise le montage d’une alimentation stabilisée de tension continue réglée sur E (ici 4.6V) en série
avec une résistance variable réglée sur r (ici 1,1  et on reprend les mesures des intensités et tensions
pour les composant utilisés au début en remplaçant la pile par cette association. On retrouve sensiblement
les mêmes points de fonctionnements pour chacun des récepteurs utilisés.
Interprétation de ce modèle en termes énergétiques
Si l’on multiplie par I les deux membres de la relation U = E – rI de manière à calculer la puissance
électrique fournie par la pile aux récepteurs, on obtient une nouvelle relation qui peut encore s’écrire
EI = rI2 + U .
Pendant une durée t quelconque, tout se passe comme si l'énergie (EIt) était prélevée à la pile et se
trouvait transférée pour partie directement de la pile à l’environnement par effet joule (rI²t) et pour le
reste, sous forme électrique vers le circuit extérieur (UIt). Le schéma énergétique de la pile est donc le
suivant :
Application à la prévision du point de fonctionnement d’un composant sur une pile de fém et de
résistance interne connues.
Détermination de la caractéristique de la lampe
Remarque préliminaire - La caractéristique de la lampe a déjà pu être tracée lors d’une activité
précédente (cf. fiche N°2 Comment faire briller une lampe sous une puissance donnée ?). Le travail
suivant s’en trouve alors raccourci.
La lampe est alimentée par un générateur de tension ajustable. Les mesures sont réalisées et traitées soit
manuellement (ampèremètre et voltmètre), soit à l'aide d'une interface (l'intensité est obtenue à partir de la
mesure de la tension aux bornes d'une résistance de 1 ohm (7,5W) placée en série dans le circuit). Elles
sont effectuées soit par les élèves à leur place (si on en a le temps et si la classe est suffisamment
motivée) soit au bureau par un binôme sous le contrôle de l’enseignant.
U
E r I

Document d’accompagnement – Physique / classe de première S © CNDP
L’essentiel est que les élèves disposent de la caractéristique de la lampe et qu’ils comprennent comment
elle est obtenue.
Commentaire - La variation de la résistance de la lampe avec la température du filament permet
d’expliquer la non linéarité de la caractéristique de la lampe et l’augmentation de la pente avec l’intensité
dans la lampe : R croît avec la température du filament (cf. document professeur N°1). Le filament de la
lampe est un conducteur ohmique et c'est parce que la température d'équilibre en régime permanent
change avec I que cette "caractéristique" présente un aspect non linéaire.
Détermination du point de fonctionnement de la lampe montée sur la pile
Le professeur explique que celui-ci doit être commun à la lampe et à la pile. Les élèves travaillent par
deux. Sur la feuille sur laquelle est tracée la caractéristique de la lampe, ils tracent la droite correspondant
au modèle de leur pile (ici E = 4,6V ; r = 1,1Ils déterminent ainsi le point de fonctionnement prévu pour
le montage de la lampe sur leur pile. Ils effectuent alors le montage et les mesures de U et I et les
comparent aux valeurs prévues.
Commentaires - Nous avons utilisé une lampe dont les valeurs nominales portées sur le culot par le
constructeur sont : 4V ; 0,3A. La construction graphique est donnée ci-dessous . E = 4,6V ; r = 1,1la
droite passe donc par les points 0A ; 4.6V et 1A ; 3,5V. Le point de fonctionnement prévu pour la lampe
montée sur notre pile correspond aux valeurs 4,25V et .030 A. (Une résolution graphique avec une
machine à calculer graphique peut aussi être effectuée ici et conduit à 4,2V et 0,3A). Les mesures
effectuées sur le montage (4.18V, 0.29A) sont très voisines des valeurs prévues.
0
1
2
3
4
5
0 0,2 0,4 0,6 0,8 1
I (A)
U (V)
Compétences du programme mises en œuvre
Compétences expérimentales et manipulatoires
- Formuler une hypothèse sur un événement susceptible de se produire ou un paramètre
pouvant jouer un rôle dans un phénomène.
- Proposer une expérience susceptible de valider ou d’invalider une hypothèse ou
répondant à un objectif précis.
- Analyser des résultats expérimentaux.
- Agir suivant un protocole.
- Faire le schéma d’une expérience.