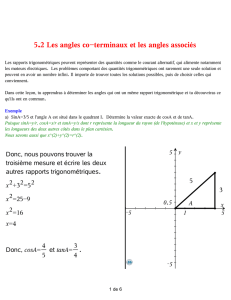
corrigé activité 2 : la conservation de châteaux

Avril 2016 Formation Mathématique-FBD
Activité 2
Rendre compte de la mobilisation des connaissances et des stratégies de résolution
mobilisées par l’élève en la contrastant aux attentes de fin de cours.
Cours ciblés pour alimenter la réflexion
Cours de représentations géométriques : MAT-3053, MAT-4153, MAT-4163, MAT-4173,
MAT-5153, MAT-5163, MAT-5173
Préalables possibles
Il faut ici distinguer les préalables selon les cours.
 Distinguer et interpréter les représentations d’un objet sous différentes vues
(projections orthogonales).
 Reconnaissance de prismes droits.
 Reconnaissance de triangles rectangles.
 Établissement et recherche de mesures manquantes à l’aide de rapports
trigonométriques.
 Établissement d’un système d’équations du 1er degré.
 Recherche d’une inconnue dans une équation du 1er degré.
 Recherche de mesures manquantes, dans un triangle quelconque, à l’aide de la loi
des sinus.
 Recherche de mesures manquantes, dans un triangle quelconque, à l’aide de la loi
des cosinus.
 Recherche de mesures manquantes à partir de l’équivalence de volumes de solides.
Intention didactique
 Résoudre la situation-problème, de type contexte nouveau, en vue de discuter avec
l’adulte des stratégies de résolution mobilisées.
Intentions de l’activité
À partir, de la mise en situation « Conservation de châteaux » et des programmes des cours
mentionnés ci-haut, compléter le tableau proposé. Le participant doit :
1) préciser pour chacune des tâches de la situation si celles-ci pourraient être proposées
à l’adulte réalisant l’un des cours donnés.
2) dans l’affirmative, identifier les savoirs qu’il pourra mobiliser.
3) identifier les stratégies de résolution dont on espère la mobilisation pour résoudre les
deux tâches du problèmes.

Page 2 sur 8
Conservation de châteaux
Quand le travail de l’arpenteur-géomètre est essentiel
Les châteaux forts, vestiges d’une autre
époque, font encore aujourd’hui la fierté
des Européens. Ces monuments sont une
preuve de savoirs faire hors pair. Il n’est
pas surprenant de tout mettre en place
pour les conserver.
La conservation de ces monuments exige
l’expertise de plusieurs professionnels.
C’est le cas de l’arpenteur-géomètre.
En effet, certains châteaux ont été bâtis à des endroits stratégiques et difficiles d’accès. Les
arpenteurs-géomètres, agissant comme vigiles du patrimoine, doivent utiliser des techniques
de mesure précises et des techniques de calcul rigoureuses afin de s’assurer que les
monuments sont sécuritaires pour les touristes qui parcourent la planète pour les visiter.
Suite à l’analyse comparative d’une année à l’autre de ces mesures, les gestionnaires de ces
sites historiques peuvent intervenir au besoin en vue de le rénover et de les maintenir un état
presque identique à celui du moment de leur construction.
Un château fort, entouré de cours d’eau, est délimité de quatre tours ayant la forme de
prismes droits à base carrée. Dans le but de s’assurer que les mouvements de sol liés aux
tremblements de terre n’ont pas trop altéré les fondations des tours, des arpenteurs-
géomètres prennent des mesures, à l’aide d’instruments, qu’ils colligent par la suite dans un
carnet.

Page 3 sur 8
Voici les résultats des mesures d’une des tours telles que consignées dans le carnet des
arpenteurs-géomètres. Ils sont accompagnés des schémas de la tour.
Hauteur de la tour
𝑚𝐾𝐿
̅
̅
̅
̅
=30𝑚
Identification
de l’angle
Mesure de
l’angle
(en degré)
∠𝐺𝐾𝐻
26,92o
∠𝐺𝐿𝐻
38,12o
Dimension de la base de la tour
𝑚𝐸𝐹
̅
̅
̅
̅
=47,17𝑚
Identification
de l’angle
Mesure de l’angle
(en degré)
∠𝐶𝐸𝐴
21,11o
∠𝐴𝐸𝐹
88,85o
∠𝐶𝐹𝐴
14,32o
∠𝐶𝐹𝐸
37,66o
∠𝐸𝐴𝐷
21,03o
∠𝐹𝐶𝐷
15,48o
Tâche 1 : Déterminez les dimensions de la tour 1.
Tâche 2 : Sachant que la hauteur des trois autres tours correspond aux trois quarts de
la hauteur de la tour 1 et sachant que les tours sont toutes de volume équivalent,
déterminez les dimensions des trois autres tours.
Tour 1 - Vue de face Nord
Tour 1 - Vue de dessus

Page 4 sur 8
Analyse des tâches
La tâche est-
elle
pertinente
pour le
cours
Tâche 1
Déterminez les dimensions de la tour 1.
Tâche 2
Sachant que la hauteur des trois autres
tours correspond aux trois quarts de la
hauteur de la tour 1 et sachant que les
tours sont toutes de volume équivalent,
déterminez les dimensions des trois
autres tours.
MAT-3053 ?
Encerclez
Oui ou Non
Identifiez les savoirs mobilisés :
- Il est possible d’adapter cette
situation pour le MAT-3053.
Pour ce faire, nous pourrions
fournir les mesures des
segments GK et GL. L’élève
pourra alors établir un système
d’équations en s’appuyant sur
le théorème de Pythagore. Par
contre, l’élève doit
obligatoirement avoir réussi le
cours MAT-3051 pour être en
mesure d’appliquer le système
d’équations et déduire toutes
les autres mesures.
Identifiez les savoirs mobilisés :
- Le schéma proposé pour
déterminer les mesures de la
base de la tour ne comporte
aucun triangle rectangle. Il y
aurait tout lieu de proposer un
autre schéma si l’on souhaite
proposer cette tâche dans le
cadre de ce cours. Dans sa
forme actuelle, cette tâche
n’est pas propice au cours.
MAT-4153 ?
Encerclez
Oui ou Non
- Reconnaissance de triangles
rectangles ou non ;
- Somme des angles intérieurs
dans un triangle ;
- Angles supplémentaires ;
- Selon la démarche des élèves,
recherche de mesures
manquantes par déduction :
o s’appuyant sur des
rapports
trigonométriques
(tangente d’un angle à
privilégier) et par
l’établissement d’un
système d’équations.
Ou
o s’appuyant sur les
rapports
trigonométriques et la
loi des sinus
- Volumes équivalents dans
son sens premier (volumes de
même grandeur) ;
- Reconnaissance de prismes à
base carrée ;
- Déduction de mesures à partir
de la formule de volume d’un
prisme ;
*Les solides équivalents ne sont pas
traités dans ce cours.

Page 5 sur 8
MAT-4163 ?
Encerclez
Oui ou Non
- Rapports trigonométriques ;
- Reconnaissance de triangles
rectangles ou non ;
- Somme des angles intérieurs
dans un triangle ;
- Angles supplémentaires ;
- Recherche de mesures
manquantes par
déduction s’appuyant sur des
rapports trigonométriques
(tangente d’un angle à
privilégier) et par
l’établissement d’un système
d’équations.
- Volumes équivalents ;
- Reconnaissance de prismes à
base carrée ;
- Déduction de mesures à partir
de la formule de volume d’un
prisme ;
- *Les solides équivalents ne
sont pas traités dans ce cours.
MAT-4173 ?
Encerclez
Oui ou Non
- Reconnaissance de triangles
rectangles ou non ;
- Somme des angles intérieurs
dans un triangle ;
- Angles supplémentaires ;
- Selon la démarche des élèves,
recherche de mesures
manquantes par déduction :
o s’appuyant sur des
rapports
trigonométriques
(tangente d’un angle à
privilégier) et par
l’établissement d’un
système d’équations.
Ou
o s’appuyant sur les
rapports
trigonométriques et la
loi des sinus.
- Il est possible d’adapter cette
situation pour permettre la
mobilisation de la loi des
cosinus. Pour ce faire, nous
pourrions enlever les mesures
des angles EAD et FCD.
- Reconnaissance de prismes à
base carrée ;
- L’adulte peut approcher le
problème en référant aux
volumes équivalents ou aux
solides équivalents :
- Déduction de mesures à partir
de la formule de volume d’un
prisme ;
Ou
- Recherche du rapport de
similitude à partir des
mesures des hauteurs des
tours.
- Recherche du volume de la
tour 1 par l’application de la
formule du volume d’un
prisme.
- Recherche du rapport de
similitude des volumes des
prismes équivalents et
déduction du volume des
autres tours puis de leurs
dimensions.