Travail à effectuer - documents a utiliser en lycee

Travaux pratiques de physique – 1 S Septembre 2003
D:\769911132.doc
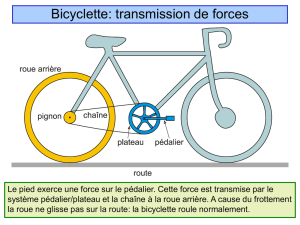
MOUVEMENT D’UNE BICYCLETTE
Objectifs : - savoir calculer une vitesse (à partir d’un enregistrement vidéo)
- savoir calculer une vitesse angulaire
- savoir définir les deux types de mouvement simples : translation et rotation
Travail à effectuer
1. A l’ordinateur
 Lancer AviMéca et charger le document vidéo « vélo » et le regarder une ou deux fois
Le pointage de trois points a déjà été effectué : - point 1
- point 2
- point 3
Les coordonnées ont été sauvegardées au format Regressi.
 Fermer AviMéca.
 Lancer Regressi et charger le fichier « Mouvement d’une bicyclette ».
En utilisant la méthode employée avec l’étude de l’équerre, faire tracer par l’ordinateur la
trajectoire du point d’un rayon de la roue par rapport à l’axe de la roue. N’afficher que les
points, sans les relier.
Appeler le professeur lorsque le travail est fait afin qu’il vous remette une feuille de documents :
- un graphe des trajectoires des trois points obtenues directement à partir du pointage.
- le graphe que vous avez à l’écran .
Noter, dans le tableau de grandeurs (« variables »), l’intervalle de temps τ qui sépare deux positions successives.
2. Questions :
2.1. Document 1
1. Dans quel référentiel sont obtenues les trajectoires du document 1 ?
2. Quels sont les deux points correspondant à une partie de la bicyclette animée d’un mouvement de translation ?
Définir le mouvement de translation. (Cette notion sera précisée ultérieurement).
3. A partir du document et de la valeur de τ, calculer la vitesse de la bicyclette.
4. Avec l’échelle suivante : 1 cm ↔ 0,5 m.s-1, tracer le vecteur vitesse du point 1 dans l’avant-dernière position du
graphe.
5. Quel la nature du mouvement du point du rayon dans ce référentiel ?
2.2. Document 2
6. Dans quel référentiel a été obtenue la trajectoire du document 2 ?
7. Cette trajectoire, dans la réalité est un cercle ; ses imperfections, sur le document, sont imputables aux
imprécisions du pointage (erreur humaine qu’il est difficile d’éliminer complètement…). A l’aide d’un compas,
déterminer le meilleur cercle possible et mesurer son rayon R.
8. Définir le mouvement de rotation.
On appelle vitesse angulaire de la roue, ω (oméga), l’angle (en radian) balayé par un rayon de la roue
en une seconde . La vitesse angulaire se mesure donc en radians par seconde : rad.s-1.On rappelle que 360 degrés (angle balayé
en un tour de roue) correspondent à 2π radians : 360 ° = 2π rad.
9. On peut admettre que le tour de roue s’effectue en un intervalle de temps T = 10 τ
Exprimer littéralement puis calculer la vitesse angulaire du point du rayon de la roue.
10. Cette vitesse est-elle la même pour tous les points de la roue ?
11. Connaissant le rayon R du cercle décrit par le point, donner littéralement la distance d parcourue par le point
en un tour (= circonférence) et en déduire l’expression littérale de la vitesse v (en m.s-1) du point..
12. En déduire la relation littérale entre la vitesse v et la vitesse angulaire ω.
Faire la vérification numérique.