Télécharger

Correction du contrôle de préparation sur les angles
Exercice n°1 ( 5 points ) :
1) Soit AOI un triangle tel que  = 35° et Ô = 55°. Déterminer la nature de AOI en
justifiant correctement.
On sait que  = 35° et Ô = 55° donc  + Ô = 90° c'est-à-dire  et Ô sont
complémentaires.
Or, si dans un triangle deux angles sont complémentaires, alors ce triangle est rectangle.
Donc AOI est rectangle en I.
2) Soit AES un triangle isocèle en E tel que  = 48°. Déterminer les mesures des angles
du triangle AES en justifiant correctement.
On sait que AES est un triangle isocèle en E
Or les angles à la base d’un triangle isocèle sont de même mesure
Donc
S
ˆ
= Â = 48°
On sait que  = 48° et
S
ˆ
= 48°
Or la somme des angles d’un triangle fait 180°
Donc  + Ê +
S
ˆ
= 180 c'est-à-dire 48 + Ê + 48 = 180 soit Ê + 96 = 180 ce qui nous
donne Ê = 84°.
3) Soit EQU un triangle isocèle en Q tel que Ê = 60°. Démontrer, en calculant les mesures
des autres angles, que EQU est un triangle équilatéral.
On sait que EQU est isocèle en Q.
Or les angles à la base d’un triangle isocèle sont de même mesure
Donc Û = Ê = 60°
On sait que Ê = 60° et Û = 60°
Or la somme des angles d’un triangle fait 180°
Donc Û + Ê +
Q
ˆ
= 180 c'est-à-dire 60 + 60 +
Q
ˆ
= 180 soit
Q
ˆ
+ 120 = 180 ce qui nous
donne
Q
ˆ
= 60°.
Le triangle EQU a ses trois angles égaux à 60° : c’est donc un triangle équilatéral.
Exercice n°2 ( 5 points ) :
1) Construire un cercle C de centre O et placer deux points A et B sur ce cercle tels que
AÔB = 70°. Déterminer les mesures des autres angles de ce triangle. Justifier.
On sait que OAB est un triangle isocèle en O
Or les angles à la base d’un triangle isocèle sont de même mesure
Donc
B
ˆ
= Â
On sait que  =
B
ˆ
et Ô = 70
Or la somme des angles d’un triangle fait 180°
Donc  +
B
ˆ
+ Ô = 180 c'est-à-dire  +  + 70 = 180 soit 2 +
70 = 180 ce qui nous donne 2Â= 110° soit  = 55° =
B
ˆ

2) Soit  et Ê deux angles complémentaires tels que la mesure de  est le double de celle
de Ê.
a) faire un schéma représentant la situation
b) Quelle est la mesure de chaque angle. Justifier.
On sait que  et Ê sont complémentaires et  = 2Ê
Or deux angles complémentaires ont pour somme 90°
Donc  + Ê = 90 c'est-à-dire 2Ê + Ê = 90 ( car  = 2Ê ) soit 3Ê = 90 ce qui
nous donne Ê = 30°.
Puis, comme  = 2Ê, on en déduit que  = 2 × 30 = 60°
Exercice n°3 ( 5 points ) : (D3)
x D3 y
A (D1)
(D1) 56°
z 130°
B v (D2)
(D2) 56°
t
Fig 1 u Fig 2
1) En utilisant les données de la figure 1 et sachant que les droites (D1) et (D2) sont
parallèles, déterminer en justifiant :
a) la mesure de l’angle xAy
Les angles xAy et zAB sont opposés par le sommet.
Or deux angles opposés par le sommet sont de même mesure
Donc xAy = zAB = 130°
b) la mesure de l’angle tBx
On sait que zAx et xAy sont supplémentaires
Or deux angles supplémentaires ont pour somme 180°
Donc zAx + xAy = 180 soit zAx + 130 = 180 ce qui nous donne zAx = 50°

On sait que zAx et tBx sont correspondants et les droites (D1) et (D2) sont
parallèles
Or, lorsque les droites qui déterminent deux angles correspondants sont parallèles,
alors les angles correspondants sont de même mesure
Donc, les angles correspondant zAx et tBx sont de même mesure soit tBx = 50°.
c) la mesure de l’angle uBv
Les angles uBv et xBt sont opposés par le sommet.
Or deux angles opposés par le sommet sont de même mesure
Donc uBv = xBt = 50°
2) En utilisant les données de la figure 2, déterminer si les droites (D1) et (D2) sont
parallèles. Justifier votre réponse.
On sait que :
 Sur cette figure sont représentés deux angles en situation d’angles
correspondants déterminés par les droites (D1) , (D2) et la sécante commune
(D3)
 ces deux angles correspondants mesurent 56° chacun.
Or, si deux angles correspondants sont de même mesure, les droites qui les
déterminent sont parallèles.
Donc les droites (D1) et (D2) sont parallèles.
Exercice n°4 (5 points ) :
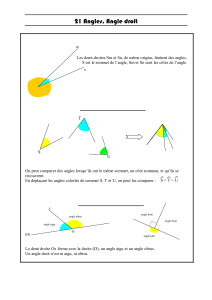
Construire, si possible, l’angle décrit et dire s’il est aigu ou obtus ( justifier ) :
a) un angle complémentaire à un angle aigu
L’angle aigu est l’angle orange. Son complémentaire
est l’angle vert. L’angle vert est un angle aigu.
b) un angle supplémentaire à un angle aigu.
L’angle aigu est l’angle orange. Son
supplémentaire est l’angle vert. L’angle vert est
un angle obtus.

c) un angle complémentaire à un angle obtus
Deux angles complémentaires ayant pour somme 90°, on ne peut pas trouver un angle
complémentaires à un angle obtus car la mesure d’un angle obtus est supérieure à 90°.
d) un angle supplémentaire à un angle obtus
L’angle obtus est l’angle orange. Son
supplémentaire est l’angle vert. L’angle vert est un
angle aigu.
e) un angle Ô opposé par le sommet à un angle  et Ô et  complémentaires.
Les angles  et Ô sont opposés par le sommet, donc
Ô = Â ( car deux angles opposés par le sommet sont de
même mesure ).
De plus, les angles  et Ô sont complémentaires donc la
sommet de leur mesure doit faire 90°. Comme  = Ô, on en
déduit que  = Ô = 45°.