Deux petits problèmes concernant les angles et leur mesure :

Classe de 6ème Devoir Maison de maths n°4
Les notions de la classe de sixième (mesures d'angles au rapporteur, tracés de triangles, proportionnalité) suffisent à répondre aux questions
posées. Il s'agit d'un travail d'exploration et de présentation. Le soin est important, l'écriture notamment doit être belle et régulière...
1) Triangles iso-zigzags
Ce sont des triangles isocèles dans lesquels ont peut construire un zigzag : une ligne brisée faite de
segments de même longueur, partant du côté principal, passant alternativement par les côtés égaux et se
terminant sur le sommet principal.
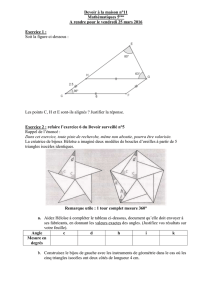
L'illustration montre un triangle iso-zigzag ABS
contenant un zigzag constitué de huit segments de
même longueur. Pour réaliser un tel triangle l'angle
principal
ASB
doit mesurer 12° (180÷15). Les
autres valeurs de l'angle principal pour obtenir des
triangles iso-zigzags sont données dans le tableau ci-
dessous.
Nombre de segments dans le zigzag 2345678
Angle principal (en °) 180÷3 180÷5 180÷7 180÷9 180÷11 180÷13 180÷15
a) Construire au moins deux triangles iso-zigzag différents (par exemple avec 3
et 4 segments dans le zigzag, mais on peut faire un autre choix). Prendre à
chaque fois des segments de même longueur, par exemple 5 cm.
b) Les triangles iso-zigzags ont la particularité de pouvoir s'assembler autour du
sommet principal pour constituer une belle rosace. Par exemple avec 8 segments
dans le zigzag, il faut 30 triangles (voir la figure). Tracer une telle rosace avec
un des deux triangles du a).
2) Angles d'un pentagone régulier
Un polygone régulier est un polygone dont tous les côtés ont la même longueur et les angles ont la même mesure.
Ses sommets appartiennent à un même cercle dont le centre est aussi le centre du polygone.
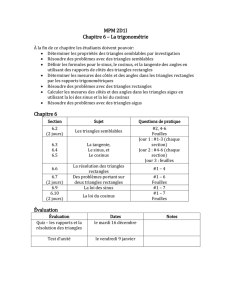
a) Le pentagone régulier peut être tracé en divisant un angle plein en cinq angles adjacents égaux.
Calculer l'angle au centre du pentagone régulier (on le notera α comme sur la figure de gauche).
Sachant que β=γ (triangle OBC isocèle en O) et que α+β+γ=180°, en déduire la
valeur des angles β, γ et δ (l'angle intérieur du pentagone).
Combien vaut la somme des cinq angles intérieurs du pentagone?
Pour tracer un tel polygone avec Scratch, on souhaite indiquer la mesure de
l'angle qui convient dans la ligne « tourner de … degrés ». Quelle est la mesure
de cet angle (noté A sur le programme de gauche) ?
Du fait de la symétrie du pentagone régulier, il y a plusieurs formes de
triangles isocèles dans cette figure : BOC, BOE, BAE et DBE.
Donner les angles de ces triangles, puis, tracer sur votre copie
ces quatre formes de triangles isocèles, en prenant 5 cm pour
chacune des bases principales.
Compléter alors le programme Scratch de droite pour qu'il trace
la figure ci-contre (le pentagone convexe bleu suivi du
pentagone étoilé rouge). Il y a deux autres angles à déterminer,
notés B et C sur le programme.
b) L'hexagone régulier ne contient pas
d'étoile régulière mais on peut, avec six
des neuf diagonales, y imbriquer deux
triangles équilatéraux qui forment
comme une étoile. Déterminer la valeur
des angles intérieurs de l'hexagone régulier convexe. Écrire un programme Scratch
qui trace un hexagone convexe régulier de 100 pixels de côtés et un des deux
triangles équilatéraux.