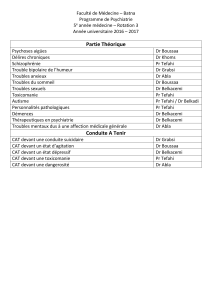
2-catégories réductibles - Mount Allison University

2
2

Set f:X→Y
X×YX
//X
f
Xf
//Y
X
X X
2
f
X/YX
//X
f
Xf
//Y
⇐=
X
X
2
2K
X2X2
X#Y
X←Z→Y2Z
Z→Z2
Z2→Z×Z Di(K)Gr(K)
Kh:U→VK

2
ZK(h, Z) : K(V, Z)→K(U, Z)
K
C1
d1//
d0
//C0
s0
oo
(d0, d1) (K)
2 (K)f:X→Y
K
1X:X→X
X2//
//X
oo
2 ∆ : K→(K)
R1 2 ∆ 2 Q
R1
f:X→YK
K
C1
d1//
d0
//C0
s0
oo
2θ:d0⇒d1
C1→C2
02θ
X2//
//X
oo
K
2θ2
An(K) 2 K∆ :
K→An(K) 2
R2 2 ∆ 2 N
R2
2K
R1R2

2KR1R2
2 2
(E)E
2 2 K
2K E
Gr(K)K
2K E 2
2
2
(K) (K)
K
2Compf2
2 (D) 2 D

2
2
2
A→B
A
A×BA//
//A
A→B
B− − > A
relation d0equivalence surjection de
sur A source A
A→B
A A →B
A− − > B
C
C0←C1→C0
A→B
A/BA//
//A
Monade sur A Foncteur bijectif sur les objets
dans les distributeurs de source A
2
//
A//(A3//A2//
//A)