application-lagrange-mse

Applications : Chapitre 4 & 5Applications : Chapitre 4 & 5
11idlimam, MSEidlimam, MSE--PCPC

ApplicationsApplications
Exercice 1
Répondre brièvement (quelques lignes suffisent) aux questions
au choix proposées ci-dessous :
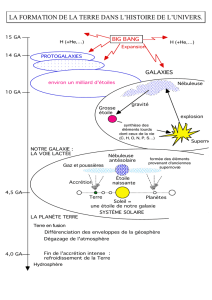
1. Définir l’année-lumière et calculer sa valeur en kilomètres.
2. Comment peut-on estimer la distance d’une étoile ou d’une
galaxie (une seule méthode, au choix) ?
3.
Comment
peut
-
on
estimer
la
vitesse
d’éloignement
d’une
22
3.
Comment
peut
-
on
estimer
la
vitesse
d’éloignement
d’une
étoile ou d’une galaxie ?
4. Comment a-t-on mis en évidence l’expansion de l’univers ?
5. Qu’est-ce que le problème de la « masse manquante » ?
6. Qu’est-ce que le rayonnement diffus cosmologique ?
7. Qu’est-ce que la nucléosynthèse primordiale ?
idlimam, MSEidlimam, MSE--PCPC

ApplicationsApplications
1. Définir l’année-lumière et calculer sa valeur en
kilomètres.
33idlimam, MSEidlimam, MSE--PCPC

ApplicationsApplications
2. Comment peut-on estimer la distance d’une étoile ou d’une
galaxie (une seule méthode, au choix) ?
Méthode de la parallaxe
(pour les étoiles pas trop
éloignées) : on compare les
positions apparentes de
l’étoile en été et en hiver,
la luminosité intrinsèque
de certaines étoiles
variables (céphéides) est
connue, donc si on en
44idlimam, MSEidlimam, MSE--PCPC
l’étoile en été et en hiver,
un calcul trigonométrique
donne la distance de
l’étoile connaissant la
distance terre-soleil.
connue, donc si on en
repère une dans une
galaxie, sa luminosité
apparente permet de
calculer sa distance.

ApplicationsApplications
3. Comment peut-on estimer la vitesse d’éloignement d’une étoile ou d’une
galaxie ?
Par l’effet Doppler : les raies d’émission ou d’absorption dans le spectre
d’une étoile ou d’une galaxie nous parviennent avec un décalage de
longueur d’onde  .
Est directement relié au rapport
v
55idlimam, MSEidlimam, MSE--PCPC
Est directement relié au rapport
v
c
4. Comment a-t-on mis en évidence l’expansion de l’univers ?
Hubble a observé que la vitesse d’éloignement des galaxies est quasiment
proportionnelle à leur distance. Cette relation n’est pas explicable par les lois
physiques classiques, notamment l’attraction gravitationnelle.