Statique des fluides (Ex)

PCSI 2 Statique des fluides
2016 – 2017 1/6
STATIQUE DES FLUIDES
I Considérons un océan en équilibre isotherme.
La masse volumique de l'eau varie avec la pression selon la loi : ρ = ρo [1 + a (P - Po)] où a = 10-10 Pa-1.
La profondeur est notée z. Pour z = 0, P = Po = 105 Pa et ρ = ρo = 103 kg.m-3.
1) Donner la loi P(z).
2) Que devient cette loi pour des profondeurs faibles?
3) Application numérique : calculer P(exact) et P(approchée) pour z = 1 km. Quelle est l'erreur relative commise en utilisant la
loi approchée?
Réponse :
P = Po + e
ρ
ogaz - 1
a
; P = Po + ρogz; ΔP/P = 0,05%.
II Une demi-sphère de rayon R repose sur le fond d'un récipient rempli sur une hauteur h > R d'un liquide de masse volumique ρ.
Le fond du récipient est percé d'une petite ouverture de façon qu'à l'intérieur de la demi-sphère la pression soit égale à la pression
atmosphérique.
Calculer la force minimale que doit exercer un opérateur extérieur pour soulever la demi-sphère, le récipient étant solidement fixé au
sol.
Réponse : 2 π R2 ρ g ( h/2 – R/3 ).
III Un mur plan est constitué de deux pavés de même largeur a et de hauteurs
respectives h' et h". Le réservoir situé à sa gauche est rempli d'eau (fluide supposé
incompressible de masse volumique µ). De l'autre côté des pavés et au-dessus de
l'eau, l'air impose une pression Po uniforme. On veut choisir le rapport h"/h’ pour
que les résultantes F' et F" des forces de pression subies par les deux pavés soient
égales.
1) Prévoir sans calcul si on doit prendre h' > h" ou h' < h".
2) Calculer le rapport h"/h’ convenable.
Réponse : h"/h’ = 1 +
€
2
.
IV On considère un fluide de masse volumique ρ, pouvant dépendre éventuellement de la pression, en équilibre dans le champ de
pesanteur terrestre uniforme
€
!
g
et occupant le demi-espace z positif; la surface libre est le plan xOy et le demi-espace z négatif est à la
pression atmosphérique uniforme Po.
1) Le liquide est de l'eau supposée, dans un premier temps, incompressible. Déterminer la relation donnant l'expression de la
pression en un point de profondeur z en fonction de Po, ρ, g et z.
Application numérique : déterminer la pression à une profondeur de 30 m si Po = 105 Pa, ρ = 103 kg.m-3, g = 9,81 m.s-2.
2) Le liquide n'est plus supposé incompressible, mais caractérisé par son coefficient de compressibilité isotherme χ =
€
1
ρ
d ρ
dP
supposé constant.
Déterminer la masse volumique ρ en un point du liquide en fonction de la pression P en ce point, de la masse volumique ρo du
liquide sous la pression atmosphérique et de Po.
3) En déduire l'expression de la pression en fonction de z.
Retrouver l'expression de la question 1) lorsque χ tend vers 0.
Application numérique : déterminer la pression à une profondeur de 30 m si χ = 5.10-10 Pa-1, ρo = 103 kg.m-3. Conclure.
Réponse : ρ(P) = ρo eχ(P - Po); p(z) = Po -
€
1
χ
Ln ( 1 - ρo g χ z ).
h'
h"
Eau
Air (pression Po)

PCSI 2 Statique des fluides
2016 – 2017 2/6
V Un hommage à Teisserenc de Bort
Données
Constantes :
Constante des gaz parfaits : R = 8,32 J.K-1.mol-1
Accélération de la pesanteur : g =9,8 m.s-2
Masses :
Masses molaires (en g.mol-1):
Mair = 29; MH2 = 2
Si le premier ballon sonde au dihydrogène est dû à Gustave Hermitte et Georges Besançon (1892), c'est incontestablement à
l'ingéniosité et à la ténacité de l'atypique Léon Teisserenc de Bort (1855-1913), que nous devons la mise au point des techniques
d'investigation par ballon-sonde et la première cartographie atmosphérique.
On note (Oz) l'axe vertical ascendant, z = 0 au niveau du sol.
€
g
= - g.
€
uz
Etude de la troposphère
La troposphère est la partie de l'atmosphère terrestre inférieure à 10 km.
On la considère comme un gaz parfait de pression p(z), de température T(z) et de volume massique v(z). Au sol, on a la pression po et
la température To.
Elle est en équilibre thermodynamique et mécanique et obéit à la loi polytropique empirique :
p-k(z) .T(z) = po-k. To avec k = 0,15 loi (1)
1) Questions préliminaires
a) Comment peut-on qualifier la transformation correspondant au cas k = 0 ?
b) Définir les mots "homogène" et "isotrope". Caractérisent-ils la troposphère ?
c) Donner l'équation d'état d'un gaz parfait liant p(z), v(z), R, Mair et T(z). loi (2)
d) Exprimer la loi de la statique des fluides avec g, dp/dz et v(z). loi (3)
2) Détermination du gradient thermique
a) Le gradient thermique est
€
grad
(T(z)) = - δ
€
uz
. Déduire δ en fonction de k, Mair, g et R à partir des lois ( (1), (2) et (3) ).
Calculer numériquement δ.
b) Donner la loi de variation T(z) en fonction de To, δ et z.
3) Evolution du volume d'une quantité de gaz constante
On considère une quantité constante de n moles de gaz parfait à l'altitude z qui évolue dans la troposphère. On note V(z) le volume
qu'elle occupe à l'altitude z et Vo son volume au sol.
Déterminer la loi
€
V(z)
Vo
en fonction de δ, z To et k.
La troposphère fut dénommée ainsi en 1902 par Léon Teisserenc de Bort à partir de la racine "tropos", le changement. Il
découvrit aussi la stratosphère.
Ascension d'un ballon sonde
Le ballon sonde dégonflé et instrumenté a une masse totale mB = 1,2 kg. On gonfle au sol son enveloppe avec no moles de
dihydrogène. Son volume est alors Vo.
L'enveloppe reste fermée tant que son volume V(z) < Vmax = 10 Vo.

PCSI 2 Statique des fluides
2016 – 2017 3/6
Lorsque V(z) = Vmax, l'enveloppe se déchire et le ballon retombe sur le sol.
4) Quels sont les avantages et les inconvénients du dihydrogène ?
5) Phase ascensionnelle à enveloppe hermétiquement fermée
Sur ce ballon s'exerce une force de frottement
€
F
frottement .
La force totale s'exerçant sur le ballon est ( F - mB.g )
€
uz
+
€
F
frottement .
a) En effectuant un bilan des forces, déterminer le terme F en fonction de no, g, MH2 et Mair.
b) Calculer la valeur minimale nmin de no pour que le ballon décolle .
c) On admet le modèle de troposphère précédent. Durant l'ascension, on peut considérer que la pression et la température sont
quasiment identiques à l'intérieur et à l'extérieur du ballon.
Calculer h, altitude maximale atteinte en prenant To = 293 K.
Commenter le résultat.
6) Etude qualitative dans le cas d'une petite déchirure
Dans le cas d'une petite déchirure, le ballon ne retombe pas instantanément au sol. Il se vide lentement de son gaz. On propose une
simulation graphique de sa descente :
Compléter les graphes F(t) et z(t) du document réponse fourni avec le sujet en n'oubliant pas d'y reporter votre nom.
La représentation est qualitative, mais un soin particulier doit être apporté afin de respecter les lois de la physique étudiées
précédemment.
Les actuels ballons sont radio-sondes depuis 1927. Le problème de la récupération du matériel est ainsi secondaire. L'altitude
atteinte par ce type de ballon est de l'ordre de 25-30 km. Ils sont depuis une dizaine d'années remplis d'hélium.
Réponse : pv = RT/Mair; dp/dz= - g/v; δ = Mair g k/R; T = To - δ z; V/Vo = ( 1 -
€
δ
To
z )1-1/k;
F = ( Mair - MH2 ) no g; nmin =
€
mB
Mair −MH2
; h =
€
To
δ
1−10k k −1
( )
.

PCSI 2 Statique des fluides
2016 – 2017 4/6
VI Un glaçon de forme cylindrique (hauteur h = 3 cm, rayon R = 1 cm, masse volumique ρS = 0,92.103 kg.m-3, température 0°C) flotte
à la surface de l’eau (masse volumique ρL = 1.103 kg.m-3, température 0°C). On appelle a la hauteur à l’air libre (figure 1).
1) Rappeler le théorème d’Archimède.
2) Déterminer le rapport a/h en fonction des masses volumique ρL et ρS. Application numérique.
3) Quelle force doit-on exercer verticalement avec l’extrémité d’une paille pour maintenir ce glaçon à la lisière de la surface de
l’eau (figure 2) ? Application numérique (g = 9,81 m.s-2).
4) On rempli le verre à ras bord (figure 3). Le glaçon ayant fondu, le verre déborde-t-il ? On justifiera précisément le comportement
du niveau d’eau.
Réponse : a/h = 8% ; F = 7,4 mN.
VII Retenue d’eau par un barrage
1) Un barrage plan (figure 1) permet de réaliser une retenue d’eau sur une hauteur H et une largeur L.
Déterminer les composantes Fx et Fz de la résultante des forces de pression qu’exerce l’eau sur le barrage (la pression de l’air est Po,
la masse volumique de l’eau est constante et est notée ρ, l’accélération de la pesanteur est uniforme et est notée g).
2) Le profil du barrage est modifié (figure 2); il correspond à une courbe (C) d’équation z = f(x).
a) Même question que précédemment avec les mêmes hypothèses ; on donnera Fz sous la forme d’une intégrale en x.
b) Application à un profil parabolique d’équation
€
z=1
h
x2
.
Réponse :
€
Fx=LH P
o+
ρ gH
2
⎛
⎝
⎜ ⎞
⎠
⎟
et
€
Fz=0
;
€
Fx=LH P
o+
ρ gH
2
⎛
⎝
⎜ ⎞
⎠
⎟
et
€
Fz=−L Po+ ρ g H −f(x)
( )
[ ]
dx
0
xo
∫=−LHh Po+2
3
ρ gH
⎛
⎝
⎜ ⎞
⎠
⎟
.
VIII Atmosphère
L’atmosphère terrestre est supposée en équilibre, formée d’air considéré comme un gaz parfait de masse molaire M = 29 g.mol-1. La
pression atmosphérique au sol est Po = 1,01.105 Pa.
1) Un modèle simple, mais discutable, consiste à considérer que la température atmosphérique est uniforme, de valeur To = 283 K
dans le domaine d’altitude envisagé.
Le champ de pesanteur est uniforme de module g = 9,8 m.s-2. Constante des gaz parfaits : R = 8,314 J.K-1mol-1.
Exprimer la loi P(z) décrivant l’évolution de la pression atmosphérique P avec l’altitude z décomptée à partir du sol.
h
a
Figure 1
h
Figure 2
F
Figure 3
h
a
Figure 1
H
O
g
z
x
Figure 2
z
x
O
H
dz
(C)
dx
ds
α
dF
M
α
xo

PCSI 2 Statique des fluides
2016 – 2017 5/6
A quelle altitude cette pression serait-elle divisée par deux par rapport à sa valeur au sol ?
2) La prise en compte de la variation de la température avec l’altitude amène à modifier l’expression P(z). En prenant le niveau de
la mer comme altitude de référence z0, et en prenant pour l'atmosphère un état moyen défini par l'atmosphère normalisée type
OACI (Température au sol 15°C = 288,15 K, pression au sol 1013,25 hPa, gradient vertical de température 0,65 K pour 100 m), on
obtient la formule internationale du nivellement barométrique donnant la pression P(z) exprimée en hectopascals (ou millibars) à
l'altitude z exprimée en mètres :
€
P(z)=1013,25 1−0,0065.z
288,15
⎛
⎝
⎜ ⎞
⎠
⎟
5,255
.
Ce modèle est construit à partir d’une description dite polytropique de l’atmosphère selon laquelle pression et température sont
reliées par une loi de forme : P(1 – k)
.Tk = Cste.
A partir des informations précédentes, déterminer la valeur du coefficient polytropique k menant à l’expression numérique P(z)
proposée.
Réponse : 5,7 km ; 1,235.
IX Une cloche cylindrique de masse m, dont l’épaisseur des parois est négligeable, est
renversée puis plongée verticalement dans une cuve remplie d’eau. On désigne
respectivement par S et Ho la section et la hauteur du cylindre, par ρ la masse
volumique de l’eau et par po la pression atmosphérique extérieure.
La cloche s’enfonce dans le liquide en emprisonnant un volume d’air initial égal à son
volume intérieur (cf. figure ci-contre). La répartition de la masse de la cloche est telle
que dans son état d’équilibre final, elle flotte en restant verticale.
On négligera la masse volumique de l’air devant celle de l’eau. On supposera que l’air
dans la cloche peut être assimilé à un gaz parfait, que sa pression à l’intérieur du
récipient est uniforme et qu’il subit une transformation isotherme.
On donnera les réponses en fonction des données suivantes : m, g, S, po, ρ, ρo et Ho.
1) Exprimer la hauteur h de la partie immergée du récipient.
2) Exprimer le volume V1 de l’air emprisonné dans la cloche.
3) Calculer la pression p1 de l’air de l’air dans la cloche.
4) Une vanne située dans la partie supérieure de la cloche permet d’évacuer une quantité d’air suffisante pour que la cloche
s’enfonce jusqu’à ce que la base du cylindre affleure juste la surface de l’eau dans la cuve. Calculer la pression p2 de l’air dans la
cloche.
5) Calculer le volume V2 de l’air dans la cloche.
6) La cloche vide est maintenant déposée à l’endroit sur l’eau et elle est remplie d’un liquide de masse volumique ρo > ρ .
Quel est le volume maximal VM de liquide que l’on peut mettre dans la cloche avant qu’elle coule ?
Réponse :
€
h=m
ρ S+mg mg +P
oSHo
;
€
V
1=P
oS2
mg +P
oSHo
;
€
P
1=P 2=P o+mg
S
;
€
V2=m
ρ
;
€
VM=
ρ SH o−m
ρ
o
.
X Résolution de problème : Montgolfière
Estimer la température minimale à laquelle l’air interne à l’enveloppe d’une montgolfière doit être portée pour assurer son décollage.
Données :
Le champ de pesanteur est uniforme de module g = 9,8 m.s-2.
Constante des gaz parfaits : R = 8,314 J.K-1mol-1 ; Masse molaire de l’air : M = 29 g.mol-1
Température atmosphérique au sol To = 288 K ; pression au sol Po = 1,01.105 Pa.
Masse de l’enveloppe et de la nacelle : 150 kg ; charge utile (dont brûleur et combustible) 350 kg.
Volume : Vo = 2400 m3
Réponse : 74°C.
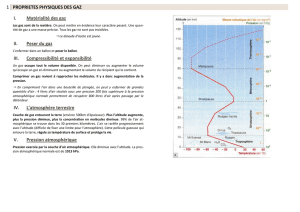
XI L’atmosphère de Titan
Saturne possède un satellite remarquable, Titan, sur lequel la sonde Huygens, véhiculée par la capsule spatiale Cassini, s’est posée
avec succès le 14 janvier 2005. Les capteurs embarqués ont permis d’enregistrer les variations de la pression et de la température en
fonction de l’altitude.
La figure suivante donne sur l’axe de gauche la pression de l’atmosphère en Pascal, en échelle logarithmique, sur l’axe de droite
l’altitude correspondante en km, en échelle non régulière, et sur l’axe horizontal la température en Kelvin en échelle linéaire. La courbe
tracée permet donc de suivre l’évolution de la température en fonction de l’altitude ou de la pression.