la composition chimique des étoiles

IV. C. - A BASSE ET MOYENNE ´ ENERGIE ET
BASSE DENSIT´ E (NUCL´ EOSYNTH` ESE).LA
COMPOSITION CHIMIQUE DES ´ ETOILES
R. Cayrel
To cite this version:
R. Cayrel. IV. C. - A BASSE ET MOYENNE ´ ENERGIE ET BASSE DEN-
SIT´ E (NUCL´ EOSYNTH` ESE).LA COMPOSITION CHIMIQUE DES ´ ETOILES. Journal de
Physique Colloques, 1969, 30 (C3), pp.C3-126-C3-131. <10.1051/jphyscol:1969320>.<jpa-
00213697>
HAL Id: jpa-00213697
https://hal.archives-ouvertes.fr/jpa-00213697
Submitted on 1 Jan 1969
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-
entific research documents, whether they are pub-
lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destin´ee au d´epˆot et `a la diffusion de documents
scientifiques de niveau recherche, publi´es ou non,
´emanant des ´etablissements d’enseignement et de
recherche fran¸cais ou ´etrangers, des laboratoires
publics ou priv´es.

JOURNAL DE PHYSIQUE
ColIoque C 3, supplément au no 11-12, Tome 30, Nov.-Déc. 1969, page C 3 - 126
IV.
C. - A BASSE ET MOYENNE ÉNERGIE
ET BAS SE
DEN SITÉ (NUCLÉO SYNTHÈ SE).
LA COMPOSITION CHIMIQUE DES ÉTOILE
s
R. CAYREL
Institut National d'Astronomie et de Géophysique, 92-Meudon, France
Résumé.
- On décrit les méthodes employées pour effectuer le passage des données de l'obser-
vation
à la compositi.on chimique des atmosphères stellaires. On indique que ce passage ne peut
se faire, dans l'écrasante majorité des cas, que moyennant une hypothèse simplificatrice dite de
l'équilibre thermodynamique local.
Un aperçu est donné des difficultés que l'on rencontre lorsque l'on veut mettre en pratique une
théorie plus générale de la formation des raies.
Quelques résultats particulièrement significatifs de l'analyse ou composition chimique des étoiles
sont donnés pour terminer.
Abstract.
- The methods used fo transform the observational data into chemical composition
of stellar atmospheres are described.
This transformation needs, in most cases, the use of a physical working assumption, called
hypothesis of local thermodynamic equilibriurn.
Some insight is given of the difficulties met when one tries to use a more general theory of line
formation.
A few results of special signifiance in the field of the nuclear composition of stars are given at
the end.
I. Introduction. - La composition chimique des
étoiles s'obtient par une analyse appropriée des
spectres stellaires
à haute résolution obtenus générale-
ment aux foyers coudés des grands télescopes. Ces
spectres sont formés d'un continu coupé de nom-
breuses raies d'absorption. Pour séparer les raies les
unes des autres, il est nécessaire de travailler avec des
résolutions de
20 000 à 40 000, ce qui, pour des sources
faibles comme les étoiles, signifie un temps d'obser-
vation élevé pour l'obtention d'un seul spectre. En
pratique, la composition chimique des étoiles plus
faibles que la magnitude
9 ne peut pas être étudiée,
même avec les plus grands télescopes.
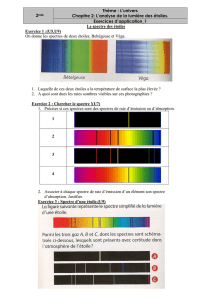
L'identification des raies est possible pour la majorité
d'entre elles (Fig. 1). Les étoiles froides montrent
surtout les raies d'atomes neutres, tandis que les
étoiles chaudes contiennent surtout les raies d'éléments
une ou denx fois ionisés.
L'intensité de chaque raie est mesurée par l'aire de la
raie divisée par le flux du continu
à l'endroit de la raie.
Cette quantité estF appelée
largeur équivalente de la
raie. Elle a les dimensions d'une longueur d'onde et
peut être visualisée comme la largeur d'une bande
rectangulaire ayant toute la hauteur du continu et
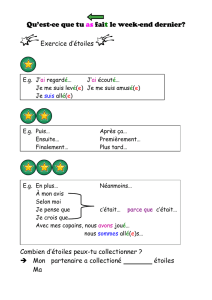
qui bloquerait le même flux que la raie (Fig.
2).
L'interprétation des largeurs équivalentes des raies
en terme de composition chimique du milieu suppose
que l'on dispose d'une description physique quan-
titative du milieu,
à la fois émissif et absorbant. Cette
description est appelée le
« modèle » de l'atmosphère
stellaire dont on cherche
à déterminer la composition
chimique. Le gaz stellaire est suffisamment opaque
pour que, seule, une mince pellicule de la matière
stellaire
à la surface de l'étoile contribue directement
au rayonnement observé. C'est cette pellicule que l'on
appelle I'atmosphère de l'étoile. La densité
p y varie
suivant la loi barométrique :
Article published online by EDP Sciences and available at http://dx.doi.org/10.1051/jphyscol:1969320

LA COMPOSITION CHIMIQUE DES ÉTOILES
C 3 - 127
ZERO
ZERO
FIG. 1. - Echantillon de spectre stellaire enregistré. En abscisse les longueurs d'onde, en ordonnée le flux de
rayonnement. Les raies les plus importantes sont identifiées (extrait de l'article
(( on the curve of growth
method
)) par L. M. Aller dans (( Abundance determinations in stellar spectra », 1. A. U. Symposium NO 26
edited by H. Hubenet, Academic Press London and New York, 1966).
FIG. la. - Portion of Spectrum of HD 168 733. Note : a) Cl II lines at left end of spectrum. b) Strong Si II
multiplet.
c) Lines of Fe 1, Fe II and Fe III.
FIG. 16. - Portion of spectrum of HD 168 733. Note : a) Four lines of Ti III. b) Two strong lines of C II.
c) Weak line showing S II in star. d) Lines of Ti 11, Fe II and CI II.
où z est l'altitude du point considérét R la c~nstante
des gaz parfaits, T la température, IL la masse molé-
culaire moyenne et
g l'accélékation de la pesanteur
à la surface de l'étoile.
La température décroît vers l'extérieur (c'est pour
cela que le spectre de raies est en absorption) et la loi
gouvernant cette décroissance%st dans la majorité
des cas déterminée par la condition qu'un élément
de matière stellaire rayonne autant d'énergie qu'il
èn absorbe (équilibre radiatif). La température absolue
des couches les plus profondes optiquement acces-
sibles n'excède pas de plus de
30 % la température
absolue des couches les plus superficielles. C'est
pourquoi dans les travaux d'il
y a dix ans, on suppo-
sait fréquemment que la température des atmosphères
stellaires était partout égale
à la température moyenne.
La valeur de la gravité
g et du flux de rayonnement
constant
F traversant l'atmosphère sont deux para-
mètres qui ne sont pas connus
a priori, mais que l'on
doit déterminer-par tâtonnements.

C 3 - 128 R. CAYREL
h
FIG. 2. -Définition de la largeur équivalente d'une raie. La
largeur équivalente est par définition l'intervalle de longueur,
d'onde
W qui, dans le cas fictif d'une absorption de 100 %,
bloquerait la même énergie que la raie.
En possession de la marche des grandeurs physiques
dans l'atmosphère, il devient possible de prédire par
des calculs théoriques la largeur équivalente d'une
raie, la concentration de I'élément produisant la raie
étant supposée connue. On calcule alors la largeur
équivalente d'une raie pour une vingtaine de valeurs
de la concentration de l'élément. On obtient ainsi la
relation entre l'abondance et la largeur équivalente
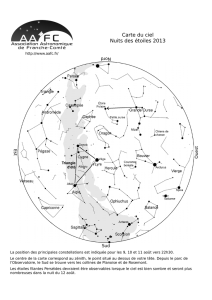
(Fig. 3, courbe de croissance), ce qui permet de faire
FIG. 3. -Courbe de croissance. La relation entre la largeur
équivalente d'une raie et la concentration
N des atomes absor-
bants porte le nom de courbe de croissance. Les abscisses et les
ordonnées sont logarithmiques. Les difféxentes parties
AB, BC
et CD de la courbe sont comnientées dans le texte.
ensuite la démarche inverse, c'est-à-dire de trouver la
concentration correspondant
à une raie de largeur
équivalente donnée.
II. Formation des raies à l'approximation de l'équi-
libre thermodynamique local. - La mise en œuvre
de
ce programme ne va cependant pas sans quelques
difficultés.
L'équation de transfert qui permet de calculer l'in-
tensité émergente s'écrit
:
où IV est l'intensité monochromatique du rayonnement,
X, le coefficient d'absorption et E, l'émission spéci-
fique et ds l'élément de longueur le long de la ligne de
visée considérée
: cette équation peut être mise sous
la forme
:
en acceptant la loi de Kirchhoff :
où B,(T) est la fonction de Planck.
Mais, pour pouvoir calculer
x, il est nécessaire de
connaître la population des niveaux atomiques
à
chaque profondeur. On suppose généralement (hypo-
thèse de l'équilibre thermodynamique local) que cette
population ne diffère pas de celle de l'équilibre thermo-
dynamique
à la température du point considéré.
Cette hypothèse entraîne en fait la loi de Kirchhoff.
A supposer que l'on connaisse les constantes ato-
miques appropriées (probabilités de transitions
optiques, poids statistiques des niveaux, fonctions
de partition) on est alors en mesure de calculer le
rayonnement émergent en fonction des conditions
locales par de simples quadratures. On démontre
facilement que le flux émergent est donné par
:
00
s, = 2 . j E,(tv) Bv(tv) dt.
O
(6)
où E,(x) est la transcendante :
où B, est la fonction de Planck et où les profondeurs
sont exprimées au moyen de la variable
(( profondeur
optique
D définie par
00
tV = %,,di. (8)
z

LA COMPOSITION CHIMIQUE DES ÉTOILES
C 3 - 129
Le moyen le plus économique de faire la quadrature
exprimée par
(6) est d'utiliser une formule de Gauss
à un point et un poids, ce qui donne l'approxima-
tion
:
6, LX nB, (t, = 3) .
(9)
rigoureuse lorsque B(tv) est fonction linéaire de t,,
et approchée dans les autres cas. Cette approximation
est, en tout cas, suffisante pour expliquer que les raies
sont en absorption
: entre les raies S,est égal à nBv à
la profondeur optique 213 dans le continu, ce qui est un
point plus profond, donc plus chaud, donc avec une
valeur de
B, plus grande que dans une raie où la grande
opacité fait que l'on observe
B, plus en surface, à une
valeur inférieure de la température, qui décroît vers
l'extérieur.
Une difficulté dans le problème de la formation des
raies est celui de la connaissance exacte des mécanismes
d'élargissement des raies. La largeur équivalente d'une
raie dépend en effet de la répartition de I'absorption
autour de la longueur d'onde
A, du centre de la raie.
Plus l'absorption est concentrée autour de A,, moins
elle contribue
à la largeur équivalente puisque le flux
ne peut pas décroître au-delà d'un plancher
:
quelle que soit l'importance de I'absorption sélective
due
à la raie (phénomène de saturation). La répartition
de I'absorption autour de
A, est en fait due aux causes
d'élargissement suivantes
:
a) agitation thermique des atomes absorbants ;
b) mouvements aléatoires dans l'atmosphère ;
c) perturbation de l'atome absorbant par ses voisins
(dans les atmosphères denses des étoiles naines) ou
largeur naturelle de la raie (dans les atmosphères
moins denses des étoiles géantes).
Les facteurs
b) et c) ne sont pas toujours aisés à
connaître avec précision. Les différentes parties de la
figure
2 reflètent essentiellement la prédominance de
l'une des causes d'élargissement énumérées ci-dessus.
La partie
AB est celle où la saturation ne se fait
pas encore sentir, la largeur équivalente est alors
simplement proportionnelle
à la concentration de
l'absorbant. La partie BC est celle de raie dont la
partie centrale est située avec les facteurs d'élargisse-
ment
a) ou 6) dominants.
La répartition de I'absorption autour de
A,, est alors
sensiblement gaussienne et il faut beaucoup augmenter
la concentration pour gagner relativement peu sur la
largeur efficace de I'absorption.
Enfin, la partie CD est dominée par un élargissement
du type c). Les ailes de la raie ont un profil de Lorentz
en
AA-2 et la largeur équivalente croît proportionnel-
lement
à la racine carrée de la concentration.
III. Théorie générale de la formation des raies.
La composition chimique des étoiles a été obtenue
jusqu'ici exclusivement en utilisant l'approximation
de l'équilibre thermodynamique local définie dans la
section précédente.
Cependant, il convient de souligner que cette
« pro-
cédure
» n'est pas rigoureuse. Le milieu que nous
considérons est, en effet, ouvert sur un espace duquel
il ne reçoit pratiquement aucun rayonnement. Cette
circonstance entraîne l'existence d'un gradient de
température et l'on peut montrer que l'équilibre ther-
modynamique local serait justifié
à la condition que la
distance moyenne
A parcourue par un photon entre
sa production thermique et sa destruction thermique
(entre temps il progresse par marche au hasard n'étant
soumis qu'à des processus de diffusion) soit suffisam-
ment petite pour que la variation de température sur
cette distance puisse être négligée.
De plus, l'équilibre thermodynamique local tombe
aussi en défaut lorsqu'un photon produit thermique-
ment a une probabilité appréciable de s'échapper du
milieu par la face
« ouverte » sans être détruit thermi-
quement par une collision de seconde espèce.
En fait, ni l'une ni l'autre de ces conditions ne sont
remplies et il est nécessaire de remplacer l'hypothèse
de l'équilibre thermodynamique local par celle que les
processus de peuplement et de dépeuplement des
niveaux s'équilibrent et conduisent
à un état station-
naire du milieu.
A ces conditions, il faut joindre les
équations du transfert du rayonnement dans toutes
raies connectant les niveaux de l'atome considéré.
Dans toute sa généralité ce problème est d'une
extrême complexité. J'indiquerai la forme relativement
simple qu'il prend dans le cas d'un atome qui aurait
seulement deux niveaux.
Appelons
:
N, la concentration des atomes au niveau inférieur,
N, la - - supérieur,
A,, la probabilité de transition spontanée d'Einstein,
BI, le coefficient d'Einstein d'excitation radiative,
C,, la probabilité de désexcitation par choc du niveau
supérieur,
@, la distribution de I'absorption en fréquence autour
du centre de la raie,
O l'angle que fait Ia direction en propagation du
rayonnement avec la normale ascendante dans
l'atmosphère,
9