Chapitre 1 - physique

Chimie chapitre1 TSI2_2015_2016
Chapitre 1 : chimie structurale
I- L’atome
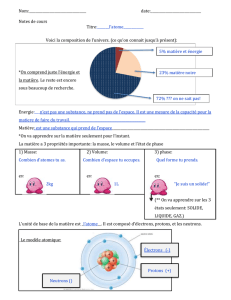
L’atome est constitué :
- D’un noyau contenant des protons et des
neutrons. Les protons (chargés et les
neutrons (neutres) sont des nucléons
- De particules à l’extérieur du noyau : les
électrons (chargés  
L'atome dans son état fondamental est électriquement
neutre : Nombre de protons = Nombre d’électrons
Un atome est noté  , où :
-  est le symbole chimique de l’atome.
-  est le numéro atomique de l’élément
correspondant au nombre de protons
-  est le nombre de masse c’est-à-dire le nombre
de nucléons. Le nombre de neutrons  vérifie
alors :     
Les isotopes d'un élément possèdent :
- le même nombre de protons (sinon ce ne serait pas
le même élément)
- un nombre de neutrons différents : même Z mais A
différent.
II- Mole et masse molaire
Une mole d’une espèce donnée correspond à une
quantité de   de cette espèce.
 Ce nombre correspond également au nombre
d’atomes qui constituent 12g de carbone  et
est appelé nombre d’Avogadro, noté 
 Soit un échantillon de matière d’un élément
donné de masse  et dont la masse molaire est
. Alors le nombre de moles, noté  et exprimé
en , contenu dans cette échantillon est donné
par :  
Représentation classique de l’atome
Propriétés de quelques particules
Particule Masse Charge électrique
Proton
Neutron
Electron
Représentation symbolique des 3 isotopes de l’élément
hydrogène
Retour sur la définition du nombre d’Avogadro
La masse d’un atome est dû essentiellement à celle de
son noyau. Il est donc logique que l’on définisse sa
masse à partir de A en effectuant une moyenne des
masses atomiques de ses isotopes (en tenant compte de
leur abondance relative). Soit, pour un composant 
quelconque, une masse atomique exprimée en unité de
masse atomique donnée par : 
  . Avec :
′
Le nombre d’atomes compris dans 12 g de carbone 
s’identifie au nombre d’Avogadro noté 
′
Si on écrit 
′
′
′
′
soit 
   mesure la masse atomique d’un élément en unité
de masse atomique ( et mesure également la masse
molaire de cet élément en  
Commentaire [A1]:
La description de
l’infiniment petit nous amène, en observant
la diffusion d’un électron par un proton, à
voir que les nucléons sont eux même
constitués de particules élémentaires : les
quarks.
C’est d’ailleurs l’interaction forte entre les
quarks qui assurent la cohésion du noyau en
s’opposant à la répulsion coulombienne
entre les protons.
A noter que l’interaction entre quarks met
en jeu une particule médiatrice de
l’interaction forte : le gluon.
A noter aussi que protons et neutrons
(constitués de quarks) sont donc sensibles à
cette interaction de contact
Commentaire [A2]:
On peut alors
s’interroger sur l’origine de la relative
stabilité de certains atomes !
Il y a une compétition entre l’attraction de
l’interaction forte et la répulsion
coulombienne entre les protons.
- Si   on peut avoir une
compensation parfaite, l’édifice est
stable
-   la compensation n’est pas
parfaite et le noyau se désintégrera.
Même si   la situation n’est pas
stable car le neutron est légèrement plus
lourd que le proton. L’interaction faible
permet de dissiper « le trop » d’énergie
de masse     
- l’édifice ne
peut même pas se former
Commentaire [A3]:
Il peut être
intéressant de connaître l’origine de la
matière : la nucléosynthèse primordiale.
- 10s après le big bang    ,
protons, neutrons, électrons, photons
sont déjà présents. L’interaction forte ne
permettait pas, à cette température, de
maintenir proton et neutron (les photons
pouvant rompre cette liaison)
-Après 3min, la température a diminué et
les premiers atomes de deutériums ont
pu se former ainsi que les premiers
noyaux légers (hélium      ,
lithium      , béryllium
     . Avec l’expansion, le
milieu est alors dilué et la
nucléosynthèse s’est arrêtée
-Après 3 milliards d’années, la
gravitation a permis l’agglomération
d’atomes légers, cette condensation
s’accompagne d’une augmentation de la
température ce qui permet les réactions
de fusions nucléaires (les noyaux ont
alors assez d’énergie pour traverser la
barrière coulombienne). Ces fusions
libèrent de l'énergie (pression de
radiation) permettant d'éviter
l'effondrement de la structure sous
l'action de la gravité : création d’étoiles.
Ce sont dans ces étoiles que les premiers
éléments chimiques se sont formés
jusqu'au fer (élément le plus stable).
-La fusion des atomes conduit à une
contraction de l’étoile puis à son
explosion (supernova) qui va permettre
au fer de capturer des neutrons
conduisant ainsi à l’atome naturel le plus
lourd l’Uranium (les atomes les plus
lourds sont fortement instable car trop
grand)

Chimie chapitre1 TSI2_2015_2016
III- Quelques résultats de chimie quantique
L’orbitale atomique est associée à une localisation
spatiales des électrons. Pour définir une orbitale
atomique, il faut trois nombres quantiques :
- Le nombre quantique principal  : il peut prendre
toutes les valeurs positives entières à l’exclusion
de zéro.
- Le nombre quantique secondaire ou azimutal ℓ : La
théorie et l’expérience montre que ℓ peut avoir
toutes les valeurs entières de à inclus
- Le nombre quantique magnétique 
ℓ
: la théorie et
l’expérience montrent que 
ℓ
peut avoir toutes les
valeurs entières entre  ℓ et  ℓ incluant le zéro.
Etablir la configuration électronique d’un atome dans
l’état fondamental (c’est-à-dire en absence de toute
excitation extérieure) consiste à répartir tous les
électrons de cet atome dans les différentes orbitales
atomiques afin d’obtenir une stabilité maximale en
suivant les trois règles qui suivent :
- Règle de Klechkowsky : les sous couches se
remplissent par valeurs croissantes de . Pour
deux valeurs égales, c’est la sous couche qui a la
plus petite valeur de  qui se remplie en première.
- Principe d’exclusion de Pauli : Si deux électrons
occupent la même orbitale atomique définie par
ℓ
ℓ
, alors ils possèdent obligatoirement un état
quantique magnétique de spin opposé. Cet état
quantique magnétique est repéré par le nombre
quantique de spin  qui possède deux valeurs 
ou  .
- Règle de Hund : Quand plusieurs orbitales ont la
même énergie (même  et ), les électrons tendent
à occuper le maximum d’orbitales avant de saturer
chacune d’entres elles : la configuration la plus
stable est obtenue lorsque le nombre d’électrons
ayant des spins identiques est maximal.
IV- Quelques notions sur le tableau
périodique
Sur une même ligne (appelée période), le passage d’un
élément à un autre s’accompagne d’une incrémentation
du nombre de protons : les atomes sont placés par
numéro atomique croissant.
Sur une même colonne (même groupe), on retrouve des
éléments possédant des propriétés physicochimiques
communes car associé à une même configuration
électronique des électrons de valence (électrons
appartenant à la dernière couche non saturée).
Orbitale 1s
Le cas de l’orbitale 1s se traite assez facilement en
postulant l’équation de Schrödinger. On montre alors
que la probabilité de présence de trouver l’électron
dans son état fondamental est de 95% dans une sphère
de rayon de l’ordre du rayon de Bohr (soit 50pm).
Règle de Klechkowsky
Il existe des exceptions à cette règle :
- Le cuivre possède une configuration électronique
en  au lieu de 
- Le chrome est en  au lieu de 
Exemple de l’atome d’oxygène
Dans ce cas : 
La configuration électronique de l’oxygène est donnée
par 
Evolution de quelques propriétés dans le tableau
périodique :
Colonne 1 : alcalin, colonne 2 : alcalino-terreux, colonne
7 : halogène, colonne 8 : gaz rares
0 1 2
3
électronégativité Rayon atomique Energie d’ionisation
Commentaire [A4]:
Les nombres quantiques se sont d’abord
imposés par l’expérience. Puis Schrödinger
et Dirac on élaboré l’équation de la
mécanique quantique qui, dans sa
résolution pour les problèmes
électronique, fait apparaître ces nombre.
- Le nombre quantique principal est
celui présenté par Bohr dans son
modèle planétaire : il fixe la taille de
l’orbitale atomique
-Le nombre quantique azimutal fixe la
forme de l’AO. Ce nombre quantique est
nécessaire pour fixer pleinement
l’énergie de l’électron
- Le nombre quantique magnétique
permet de fixer l’orientation de l’AO.
C’est ainsi que l’AO 2s n’est associée
qu’à une valeur de 
ℓ
et que les
orbitale 2p sont associée à 3 valeur de
ℓ
. Ce nombre quantique permet
d’expliquer l’influence d’un champ
magnétique extérieur sur les niveaux
d’énergie.
-Le nombre quantique de spin s’est
imposé d’abord expérimentalement. On
assimile alors très vulgairement
l’électron à un petit aimant ne pouvant
présenter que deux orientation
http://toutestquantique.fr/bonus/

Chimie chapitre1 TSI2_2015_2016
V- Représentation de Lewis
Une façon grossière de représenter la disposition des
électrons autour des atomes consiste à faire usage de
points pour des électrons de valence non appariés (seul
dans une case quantique) et d’un tirait pour 2 électrons
appariés.
Représentation de Lewis d’une molécule : Il faut suivre
les règles suivantes pour obtenir la représentation de
Lewis d’une molécule :
- Ecrire la notation de Lewis des atomes de la
molécule seuls
- On comptabilise la totalité N des électrons de
valence de tous les atomes de la molécule
- On divise N par deux pour avoir le nombre de
doublets liants et non liants
- Connaissant à priori l’enchaînement des
atomes, on répartit les N/2 doublets liants et
non liants afin de respecter la règle de l’octet
(4 doublets liants ou non liants entourant
chaque atome)
VI- Éléments de cristallographie
Certains solides présentent des organisations spatiales
périodiques : on parle de structure cristalline.
La formule chimique du composé est le motif, qui se
répète donc régulièrement dans les trois directions de
l’espace formant ainsi un réseau. Pour le caractériser il
suffit de repérer la figure géométrique la plus simple
permettant de reproduire toute la structure par simple
translation : c’est la maille élémentaire.
Nous supposerons à la fois la structure cristalline
comme parfaitement périodique mais aussi que les
motifs (atomes, ions ou molécules) occupent des
volumes sphériques (de rayon ) ne pouvant
d’interpénétrer : c’est le modèle des sphères dures.
Il est possible de décrire toutes les structures
cristallines avec un nombre limité de formes
mathématiques de mailles et un nombre limité de
manière de les remplir.
En connaissant le nombre  de motifs (de masse molaire
) par maille (de volume  , on peut obtenir la
masse volumique :
On en déduit aussi la compacité :
Représentation de Lewis d’un atome
Représentation de Lewis d’une molécule
Exemple  :
Motif, maille et réseau
Nombre de motifs  par maille
Commentaire [A5]:
Ou règle du duet
Commentaire [A6]:
Nous verrons en
exercice que la cristallographie utilise les
résultats de l’optique ondulatoire pour
analyser la périodicité d’une structure :
c’est la diffraction de Bragg

Chimie chapitre1 TSI2_2015_2016
Forme de la maille Mode de remplissage (ou réseau de
Bravais)
Nom de la
maille Nombre de motifs
Relation entre
et
le paramètre de
maille
Compacité
Cubique
Mode simple (ou primitif)
Cubique simple
(ou primitive)     
On a contact entre
deux motifs pour
chaque arrête :
Cubique
Mode centré
Cubique centré       
On a contact entre
3 motifs le long de
la grande diagonale
de longueur  :
Cubique
Mode faces centrés
Cubique faces
centrées     
On a contact entre
3 motifs le long de
la petite diagonale
de longueur  :

Chimie chapitre1 TSI2_2015_2016
Hexagonal
Mode Simple (ou primitif)
Hexagonal
simple (ou
primitif)
Dans la maille simple, on a :
On a c
ontact entre
tous les atomes du
losange 
Soit hauteur  de
ce prisme à base
losange (120°) :
AC est aussi
jointif :
Le volume de la maille
est 
On obtient alors
Même avec une compacité importante, on trouve des espaces inoccupés, appelée sites, dans lesquels peuvent s’insérer d’autres motifs. Par exemple dans une maille cubique en CFC, on a :
Des sites octaédriques (au centre du cube et au milieu de chaque arrête soit ) tétraédriques (au nombre de 8)
Cette notion de sites est importante pour expliquer l’existence d’alliages d’insertions ou pour expliquer la possibilité l’amélioration de la compacité d’une structure par insertion d’atomes.
A
B
C
Commentaire [A7]:
Ce sont les 2/3
d’une médiane d’un triangle équilatérale
de côté a : centre d’un des deux triangles
du losange
Commentaire [A8]:
On peut utiliser les
propriétés du produit vectoriel