Chute libre : Exercice sur le saut de Baumgartner

Thème 2 : Comprendre – Lois et modèles
Temps, Mouvement et Evolution
Le saut de Félix Baumgartner
Etude de la chute libre
Document 1 : Red Bull Stratos
Red Bull Stratos est un projet impliquant le parachutiste autrichien Felix Baumgartner. Baumgartner est
monté à 39 km dans la stratosphère au-dessus du Nouveau-Mexique (États-Unis) dans un ballon à hélium
avant d'exécuter sa chute libre dans une combinaison pressurisée et d'atterrir en parachute.
Le lancement du ballon stratosphérique a eu lieu le 14 octobre à 17 h 31, heure française, supervisé par un
centre de contrôle (mission control) basé à Roswell dans l'état américain du Nouveau-Mexique et
retransmis en direct sur internet. Le ballon atteint l'altitude de 39 045 m en un peu plus de deux heures.
Baumgartner se lance dans une chute de 4 minutes et 20 secondes, atteignant la vitesse maximale de
1 341,9 km.h-1, soit Mach 1,25 , avant d'ouvrir son parachute et de se poser sans encombres après une
chute totale de 9 minutes et 3 secondes.
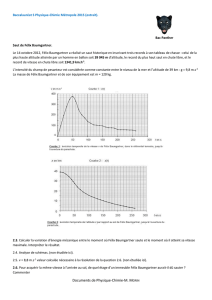
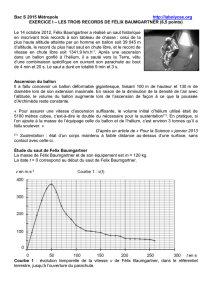
Document 2 : Evolution de la vitesse au cours du saut
http://www.youtube.com/watch?v=raiFrxbHxV0
En utilisant la vidéo de la chute de F. Baumgartner, on a relevé la vitesse (v) et l’altitude (z) toutes les 5s
pendant les 100 premières secondes de chute. Les relevés sont regroupés dans le fichier LibreOfficeCalc,
sur lequel on a tracé le graphique v = f(t) pour les 100 premières secondes de chute.
Document 3 : Rappel de seconde
En physique, on parle de chute libre d’un corps lorsque ce corps n’est soumis qu’à son poids, la force qui
l’attire vers la Terre. Tous les frottements de l’air sont alors négligeables.
Le poids d’un corps est proportionnel à la masse de ce corps. Il se calcule à partir de la relation suivante :
P = m . g
où g est appelée intensité de la pesanteur (ou gravité). Autour de la Terre, g = 9,8 N.kg-1
Problème : Déterminer pendant combien de temps la chute de Félix Baumgartner peut être considérée
comme libre ?
0
50
100
150
200
250
300
350
400
0 20 40 60 80 100 120 140 160 180 200 220 240 260
Evolution de la vitesse au cours de la chute de Félix Baumgartner jusqu'à
l'ouverture du parachute
v (m.s-1)
t (s)

On cherche à établir les équations horaires donnant l’évolution de la vitesse v(t) et de la hauteur de chute
h(t) au cours du temps en utilisant un enregistrement vidéo qui présente la chute d’une balle pendant une
durée suffisamment courte pour que toute autre action que le poids (notamment les frottements de l’air)
puisse être négligées.
 Acquisition des données à partir de la vidéo
- À partir du module vidéo du logiciel Latispro, ouvrir le fichier « Chute».
- Faire défiler les images pour repérer la première image qui montre la balle complètement visible et
libérée de l’action de la main du lanceur.
- Sur cette première image, choisir le centre d’inertie de la balle comme origine O des axes, l’axe x’x
étant horizontal et orienté vers la droite et l’axe y’y vertical et orienté vers le bas. L’origine des
dates (t= 0 s) sera associée à cette image.
- Étalonner très soigneusement l’écran au moyen de la toise
- Pointer les images jusqu’à la fin du mouvement dans l’air.
 Expression de l’ordonnée y(t) de la balle (on ne s’intéresse qu’au mouvement vertical de la balle)
- Renommer YA la grandeur acquise décrivant l’ordonnée de la balle dans le repère
- Afficher YA en fonction du temps su un même graphique
- Modéliser la courbe en choisissant convenablement le modèle.
(en cas d’hésitation, procéder à plusieurs essais et utiliser la valeur du coefficient de corrélation
pour valider le modèle ; celui-ci doit être le plus proche possible de 1)
Écrire l’équation numérique du modèle mathématique retenu :
y(t) = 4,9 . t2 + 1,6 . t + 3,5×10-3
- Déterminer graphiquement la valeur de y0 (ordonnée de la balle à t=0) ; identifier quelle terme de
l’expression ci-dessus correspondent à cette valeur.
y0 = 3,5×10-3 m
 Expression de vy(t) de la vitesse :
- A partir de y(t) modélisée en 2.3., établir l’expression de vy(t) : (calcul mathématique attendu)
vy(t) = 9,8 . t + 1,6
- Utiliser les fonctionnalités du logiciel pour créer la grandeur vy=
dt
dy
.
- Afficher le graphe représentant vy en fonction du temps dans une nouvelle fenêtre.
Nommer cette grandeur vy.
- Modéliser mathématiquement vy
- Écrire l’équation numérique retenue ; vérifier qu’elle coïncide avec l’expressions établie en 3.1..
vy(t) = 9,8 . t + 1,6
- Déterminer graphiquement la valeur de vy0 ; identifier quelle terme de l’expression ci-dessus
correspond à cette valeur.

v0 = 1,6 m.s-1
 Expression de l’accélération ay(t)
- Etablir l’expression de l’accélération ay(t) et montrer que l’accélération est constante (calcul
numérique attendu)
ay(t) = 9,8
- Utiliser les fonctionnalités du logiciel pour déterminer la valeur de ay
ay = 9,8 (valeur constante)
- Vérifier que les deux valeurs obtenues coïncident.
- Quelle valeur reconnaissez-vous ? Déterminer l’écart relatif entre la valeur déterminée
expérimentalement et la valeur reconnue
ay est l’intensité de la pesanteur g.
g correspond donc à l’accélération d’un corps en chute libre ; son unité est celle d’une accélération :
ay = 9,8 m.s-2
Signification : la vitesse d’un corps en chute libre augmente de 9,8 m.s-1 chaque seconde !
 Récapitulatif :
Remplacer les valeurs des expressions modélisées par les grandeurs g, v0 et y0
ay (t) = g
vy(t) = g.t + v0
y(t) = 1/2 . g . t2 + v0 . t + y0
En utilisant les résultats, répondre au problème posé ; expliquez la démarche.

Questions supplémentaires :
1. Lors de son saut, Félix Baumgartner a-t-il atteint une vitesse supersonique ? Justifier.
La vitesse du son est d’environ 340m.s-1. Celle-ci est bien dépassée vers la 40ème seconde de chute.
2. Les schémas ci-dessous représentent à trois instants les forces appliquées au système S lors du saut :
f modélise les frottements, P modélise le poids.
Affecter un schéma à chacune des dates : t1 = 40 s, t2 = 50 s et t3 = 60 s
Au cours de la chute, les frottements augmente lorsque la vitesse augmente :
B correspond à t1 = 40 s
C correspond à t2 = 50 s
A correspond à t3 = 60 s
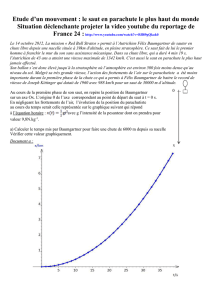
3. Déterminer l’altitude à laquelle Félix Baumgartner ouvre son parachute. En supposant que le système a
un mouvement rectiligne et uniforme après l’ouverture du parachute et jusqu’à l’arrivée au sol,
déterminer la valeur de la vitesse du système durant cette phase du mouvement. On rappelle que le
saut a duré en totalité 9 min et 3 s.
D’après le texte, on sait que le parachute s’ouvre au bout de 4min 20s soit au bout de 260s.
D’après le second graphique, on voit que l’altitude à cette date est d’environ 2500m.
Au cours de sa descente, Baumgartner parcourt donc 2500m à vitesse constante (mouvement uniforme)
pendant une durée Δt = 543 – 260 = 283 s
0
5000
10000
15000
20000
25000
30000
35000
40000
0 50 100 150 200 250 300
z (m)
t (s)
Evolution de l'altitude en fonction du temps

(Rq : 9min 3s = 543s)
La vitesse à laquelle Baumgartner atteint le sol est celle qu’il a pendant cette descente :
v = 2500/283= 8,8 m.s-1
4. Pour acquérir la même vitesse à l’arrivée au sol, de quel étage d’un immeuble Félix Baumgartner aurait-
il dû sauter ? Commenter.
Adaptation des équations horaires pour une chute libre sans vitesse initiale : h = 1/2.g.t2 et v = g.t
La durée de chute libre pour atteindre la vitesse est donc : t = v/g A.N. t = 8,8/9,8 = 0,90s
La hauteur de chute correspondante est : h = 1/2.g.t2 A.N. h = 4,0 m
Cette hauteur correspond à 1 saut du 2ème étage d’un immeuble…