TD d`électrocinétique n 3 Réponse d`un circuit linéaire du premier

Lycée François Arago
Perpignan
M.P.S.I.
2012-2013
TD d’électrocinétique no3
Réponse d’un circuit linéaire du premier ordre
à un échelon de tension ou de courant
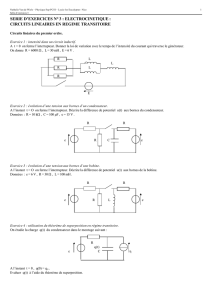
Exercice 1 - Étude d’un circuit RC.
On considère le circuit représenté figure 1. L’interrupteur Kest ouvert depuis très longtemps. A l’instant t= 0, on
ferme l’interrupteur K.
1 . Juste avant la fermeture de l’interrupteur K, donner l’expression de l’in-
tensité i2(0−) du courant électrique circulant dans le résistor de résistance R/3
en fonction des données de l’énoncé. Justifier rigoureusement votre réponse.
2 . Juste après la fermeture de l’interrupteur K, donner l’expression de l’in-
tensité i2(0+) du courant électrique circulant dans le résistor de résistance R/3
en fonction des données de l’énoncé. Justifier rigoureusement votre réponse.
3 . Quand ttend vers l’infini (régime permanent atteint), donner l’expression
de l’intensité i2(+∞) du courant électrique circulant dans le résistor de résis-
tance R/3 en fonction des données de l’énoncé. Justifier rigoureusement votre
réponse.
C
R
R/3
i2
E
K
Figure 1
4 . Montrer en utilisant les lois d’association des dipôles linéaires et l’équivalence entre les représentations de
Thévenin et de Norton d’une source réelle que le circuit est équivalent à un circuit Req Ceq série en charge dont on
précisera les caractéristiques.
5 . En déduire l’équation différentielle vérifiée par i2(t) et la résoudre.
6 . Tracer l’allure de i2(t).
Exercice 2 - Lampe au néon.
Une lampe au néon (L) présente une tension d’allumage Ua= 90 Vet une
tension d’extinction Ue= 70 V. Lorsque la lampe est éteinte, sa résistance
peut être considérée comme infinie. Lorsqu’elle est allumée, sa résistance est
r= 10 kΩ.
Lest montée dans le circuit représenté figure 2.
1 . Expliquer pourquoi la lampe émet périodiquement un flash lumineux.
2 . Déterminer la durée d’un flash et sa période d’émission.
R
CELu
Figure 2
Exercice 3 - Circuit avec bobine.
1 . A l’instant t= 0, on ferme l’interrupteur K.
1.1 . Déterminer i2(t) dans la bobine d’inductance L2.
1.2 . Déterminer i1(t) dans le résistor de résistance R1.
2 . Le régime permanent étant établi, on ouvre l’interrupteur K; déterminer
l’intensité du courant qui circule dans le circuit, puis la tension u(t).
r
R1
i1
R2
L2
K
E
u
i2
Figure 3
S. Bénet 1

Méthode 1 : Ne pas effectuer de transformations sur le circuit, écrire la loi des noeuds ainsi que les équations
de fonctionnement des dipoles présents dans les trois branches du circuit. En déduire l’équation différentielle
vérifiée par i2(t)puis la résoudre.
Méthode 2 : Transformer le circuit de façon à vous ramener à un circuit ne contenant qu’une seule maille.
1.1. :i2(t) = ER1
rR1+R2(r+R1)[1 −exp (−t/τ)] avec τ=L2(r+R1) rR1+R2(r+R1)
1.2. :i1(t) = E
rR1+R2(r+R1)R2+rR1 r+R1
exp (−t/τ)avec τ=L2(r+R1)
rR1+R2(r+R1)
2. : Rechercher préalablement les valeurs de i1(+∞)et de i2(+∞)qui serviront de nouvelles condi-
tions initiales
i2(t) = ER1
rR1+R2(r+R1)exp (−t/τ ′)
u(t) = −R2
1E
rR1+R2(r+R1)exp (−t/τ ′)avec τ′=L2 R2+R1
Exercice 4 - Circuit R L série en parallèle avec RC série.
On considère le montage représenté à la figure 4.
Le condensateur n’est pas chargé initialement et aucun courant ne circule.
At= 0, on ferme l’interrupteur K.
1 . Déterminer l’intensité i(t) qui traverse le générateur.
2 . A quelle condition cette intensité est-elle indépendante du temps ?
3 . A quelle condition la tension uest-elle nulle en permanence ?
LR1
R2C
u
K
i
E
Figure 4
Ne pas effectuer de transformations sur le circuit, écrire la loi des noeuds ainsi que les équations de fonctionne-
ment des dipoles présents dans le trois branches du circuit. En déduire l’équation différentielle vérifiée par i2(t)
puis la résoudre.
Réponses :
1. :i(t) = E
R1
[1 −exp (−t/τ1)] + E
R2
exp (−t/τ2)avec τ1=L
R1
et τ2=R2C
2. :R1=R2et L=R2
1C
3. :R1R2=L
C
Exercice 5 - Échange d’énergie entre deux condensateurs.
Les condensateurs sont initialement déchargés.
Pour t < 0, l’interrupteur est d’abord relié à la borne 1et on considère que le
régime permanent est atteint.
1 . Déterminer la valeur de la charge q1(0−) portée par le condensateur de
gauche à l’instant t= 0−.
A l’instant t= 0, on bascule l’interrupteur de la position 1à la position 2.
2 . Représenter le circuit à l’instant t= 0+en indiquant les valeurs de toutes
les intensités et de toutes les tensions.
R R
K
E
C
q1C
q2
1 2
Figure 5
3 . Déterminer pour t > 0 l’évolution de la charge q2(t) du condensateur de droite.
4 . Pour t > 0, réaliser un bilan énergétique et en déduire l’énergie dissipée par effet Joule dans le résistor à la fin de
la décharge (lorsque t→ ∞ ) ?
S. Bénet 2/2