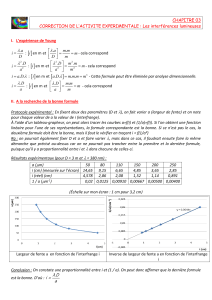
ℓ = ℓ = ℓ = ℓ =

Page 1 sur 2
Pointeur optique à laser Production : I.Akdime – JC.Bertrand – M.Moppert – J.Praud
TS Physique Ondes lumineuses : pointeur optique à laser Exercice résolu
- Enoncé -
Un pointeur optique à laser a la forme et la taille d’un gros stylo. Le faisceau lumineux qui en sort,
lorsqu’il est dirigé en direction d’un tableau, donne un point d’impact rouge très lumineux et de
petites dimensions.
Il permet à un conférencier, même lorsqu’il se trouve très loin du tableau, de pointer un endroit
précis d’un document projeté.
On veut retrouver expérimentalement l’ordre de grandeur de la longueur d’onde λ0 de la lumière
émise par le pointeur optique à laser (longueur d’onde indiquée dans la fiche technique : λ0
comprise entre 660 et 680 nm).
On utilise le montage suivant : une fente verticale, de largeur
a très petite, est placée sur le
trajet du faisceau lumineux produit par le laser et un écran est placé à la distance D de le fente.
1. Recopiez la phrase suivante en la complétant : « La tache centrale observée sur l’écran
s’appelle tache de ………………………… . Sa largeur dépend de la ………………. de la fente et de la
……………………………….. de la lumière incidente ».
2. On propose 4 expressions pour la largeur ℓ de la tache centrale :
… et on réalise 3 expériences :
Expérience Nature de la
source
Distance
fente-écran
Largeur de
la fente
Largeur ℓ de la tache
centrale
(1) Source de longueur
d’onde λ1 = 543 nm
D a ℓ1 = 3,2 cm
(2) Pointeur de longueur
d’onde λ0
D a ℓ2 = 4,0 cm
(3) Source de longueur
d’onde λ1 = 543 nm
D a3 < a ℓ3 > ℓ1
3. Par une analyse dimensionnelle, montrez qu’une des expressions est manifestement fausse.
4. À partir des expériences, déterminez les autres expressions que l’on doit éliminer. Justifiez
votre réponse et précisez les expériences prises en compte. En déduire l’expression de la largeur
de la tache centrale.
5.
a) Etablissez la relation entre ℓ1, ℓ2, λ1 et λ0.
b) Calculez la valeur numérique de λ0.
c) Ce résultat est-il en accord avec la notice technique du laser ?
(a) ℓ = a
D
λ
2 (c) ℓ =
λ
aD2
(b) ℓ = a
D
λ
2
2 (d) ℓ = D
a
λ
2

Page 2 sur 2
Pointeur optique à laser Production : I.Akdime – JC.Bertrand – M.Moppert – J.Praud
- Corrigé -
1. « La tache centrale observée sur l’écran s’appelle tache de diffraction. Sa largeur dépend de la
largeur de la fente et de la longueur d’onde de la lumière incidente ».
2. En unités S.I : l en [m] ; D en [m] ; a en [m] ; λ en [m]
Expressions : (a) en [m] ; (b) : sans unité ; (c) : en [m] ; (d) : en [m]
L’expression (b) n’est pas homogène : il faut donc l’éliminer.
3. En comparant les expériences (1) et (3), on constate que la largeur de la tache est une fonction
décroissante de la largeur de la fente.
Or les expressions (c) et (d) attestent du contraire : il faut donc les éliminer.
La seule expression à retenir est donc l’expression (a).
4.
a) Cte
a
Dl
a
D
l==⇒= 22
λ
λ
=>
2
0
1
1
ll
λ
λ
=
b) 1
1
2
0.
λλ
l
l
= soit λ0 = 543
2,3
0,4 × ≈ 679 nm
Ce résultat est en accord avec la notice technique du laser puisque : 660 nm ≤ λ0 ≤ 680 nm