Document

Thème : PHENOMENES VIBRATOIRES
Chap 2 : REFLEXION ET REFRACTION DE LA LUMIERE
1) Introduction :
La lumière est de l’énergie qui se propage sous forme de rayonnement. Dans un milieu homogène,
linéaire, isotrope (mêmes propriétés dans toutes les directions et qui ne dépend pas du temps) et
transparent, la lumière se propage en ligne droite. Le trajet de la lumière est indépendant de son sens de
propagation : c’est le principe du retour inverse.
Un rayon lumineux sera représenté par une droite.
Remarque : dans un milieu hétérogène, la lumière ne se propage plus en ligne droite mais de façon
incurvée.
Exemples :
Eau salée ou sucrée
Plus concentrée au fond
laser
Indice de réfraction
n croissant
Dans le desert
Température
croissante
et n décroissant
mirage
Vision tangentielle
aux rayons lumineux
Quand il fait très chaud et par temps ensoleillé, on croit voir sur la route de l’eau
: c’est
l’image du ciel sur la route.
N°1
N°2
N°3
N°4
laser
Semelle du fer à
repasser très chaud
Le rayon lumineux est dévié
oeil

La célérité de la lumière (vitesse de propagation) dépend du milieu dans lequel elle se propage. Le vide
est le milieu où elle se déplace le plus rapidement.
On définit l’indice de réfraction n du milieu :
m/s) (en milieu le dans lumière la de célérité
m/s) (en vide le dans lumière la de célérité
n =
n est donc sans unité et supérieur ou égal à 1.
Exemples : Milieux Célérité en m/s Indice de réfraction n du milieu
Vide 3.10
8
1
Air 3.10
8
1
Eau 2,25.10
8
1,33
Verre 1,7.10
8
à 2.10
8
1,5 à 1,76
Diamant 1,23.10
8
2,43
Dans un milieu homogène, linéaire, isotrope et transparent un rayon lumineux peut être modifié de
différentes manières : la réflexion et la réfraction.
2) La réflexion :
Diffusion : Lorsqu'une surface éclairée renvoie la lumière dans toutes les directions, on dit qu'elle diffuse
la lumière. (ex : feuille de papier blanc).
Réflexion : Lorsqu'une surface éclairée renvoie la lumière dans une direction privilégiée, on dit qu'elle
réfléchit la lumière. (ex : feuille d'aluminium, miroir…).
Utilisons un miroir. Un miroir est une surface polie réfléchissante.
i : angle d’incidence
r : angle de réflexion
air
r
i
normale
miroir
Rayon incident
Rayon réfléchi
Source S
S’
O : observateur
Feuille de papier blanc

Un observateur placé en O reçoit le rayon réfléchi qui semble provenir de S’ (image de S par rapport au
miroir).
La loi de Descartes pour la réflexion est : angle d’indicence i= angle de réfraction r
Propriétés de l’onde réfléchie : mêmes fréquence, période, longueur d’onde que l’onde incidente.
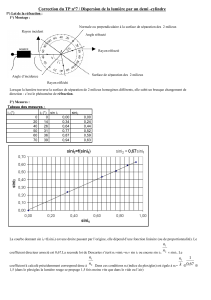
3) La réfraction :
On envoie un rayon lumineux à la surface de l'eau. On constate que les deux rayons sont dans le même
plan mais n’ont pas la même direction : le rayon est réfracté, sa direction a changé
Exp : un rayon incident dans l’air d’indice n
1
(provenant d’une lampe + une fente) arrive sur un demi
disque en plexiglas d’indice n
2
. Pour différentes valeurs de l’angle d’incidence i
1
, mesurer l’angle de
réfraction i
2
dans le plexiglas.
Comparer i
1
et i
2
. Puis calculer :
2
1
i sin
i sin
. On remarque que ce rapport est constant. Il est égal à
1
2
n
n
.
Déterminer n
2
l’indice de réfraction du plexiglas.
La loi de Descartes pour la réfraction est : n
1
sini
1
= n
2
sini
2
1
er
cas : la lumière pénètre dans un milieu plus réfringent : n
2
> n
1
:
n
2
> n
1
donc sini
2
< sini
1
soit i
2
< i
1
: le rayon réfracté se rapproche de la normale.
air
eau
i
2
i
1
normale
interface
Rayon incident
Rayon réfracté
Milieu n°1 : indice n
1
Milieu n°2 : indice n
2
> n
1
i
2
i
1
normale
interface
Rayon incident
Rayon réfracté

A la limite, quand i
1
= 90° on a : sini
2max
=
2
1
n
n
:
2
ème
cas : la lumière pénètre dans un milieu moins réfringent : n
2
< n
1
:
n
1
> n
2
donc sini
2
>sini
1
soit i
2
> i
1
:le rayon réfracté s'écarte de la normale :
A la limite, quand i
2
= 90° on a : sini
1limite
=
n
n
2
1
.
Si i
1
> i
1limite
on a réflexion totale dans le milieu n°1 :
Milieu n°1 : indice n
1
Milieu n°2 : indice n
2
< n
1
i
2
= i
1
i
1limite
normale
interface
Rayon incident Rayon réfléchi
i
1
Milieu n°1 : indice n
1
Milieu n°2 : indice n
2
< n
1
i
2
= 90°
i
1limite
normale
interface
Rayon incident
Rayon réfracté
Milieu n°1 : indice n
1
Milieu n°2 : indice n
2
< n
1
i
2
i
1
normale
interface
Rayon incident
Rayon réfracté
Milieu n°1 : indice n
1
Milieu n°2 : indice n
2
> n
1
i
2max
i
1
= 90°
normale
interface
Rayon incident
Rayon réfracté

4) Application de la réfraction : les lentilles minces :
lampe + 5 fentes : 5 rayons lumineux parallèles
Ils arrivent sur différents types de lentilles convexes et concaves, les retourner pour voir si cela change
quelque chose. Les classer par famille.
Convexes : lentilles convergentes concaves : lentilles divergentes.
lentilles minces convergentes lentilles minces divergentes
axe optique
O
F F'
espace objet espace image
sens de propagation de la lumière
axe optique
O
FF'
espace objet espace image
sens de propagation de la lumière
O : centre optique
: tout rayon arrivant sur la
lentille et passant par O la traverse sans être
dévié.
F' : foyer principal image : tout rayon parallè
le à
l'axe optique émerge de la lentille en passant par
F'.
F : foyer principal objet
: tout rayon passant par
F émerge de la lentille parallèlement à l'axe
optique.
F et F' sont symétriques par rapport à O.
F' est à droite de O.
OF
'
= f ' est la distance focale image (en mètre)
f ' > 0
La vergence est C ou V =
1
f '
en dioptries (δ)
elle
est positive
Les foyers F et F' ont la même définition que pour
les lentilles minces convergentes.
F et F' sont virtuels.
F' est à gauche de O.
OF
'
= f ' < 0
La vergence a la même définition et est négative.
Un objet dans l'espace objet est réel. Un objet dans l'espace image est virtuel.
Une image dans l'espace objet est virtuelle. Une image dans l'espace image est réelle.
conditions de Gauss : pour obtenir une image de bonne qualité il faut :
- des rayons faiblement inclinés par rapport à l'axe optique
- des rayons lumineux rencontrant la lentille au voisinage de sa région centrale.
On suppose que ces conditions sont toujours remplies pour résoudre les exercices.
Formules de Descartes :
Un objet AB de faibles dimensions est placé perpendiculairement à l'axe. On appelle A'B' l'image de AB.
On définit les notations suivantes :
Position de l’objet p =
OA
, position de l’image p' =
OA'
, distance focale
OF
'
= f ' : ces grandeurs sont
algébriques (elles peuvent être positives ou négatives).