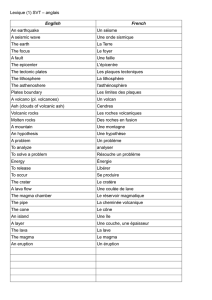
Tâches de raisonnement en logiques hybrides

Tˆaches de raisonnement en logiques hybrides
Guillaume Hoffmann
To cite this version:
Guillaume Hoffmann. Tˆaches de raisonnement en logiques hybrides. Math´ematiques [math].
Universit´e Henri Poincar´e - Nancy I, 2010. Fran¸cais. <tel-00541664>
HAL Id: tel-00541664
https://tel.archives-ouvertes.fr/tel-00541664
Submitted on 1 Dec 2010
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-
entific research documents, whether they are pub-
lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destin´ee au d´epˆot et `a la diffusion de documents
scientifiques de niveau recherche, publi´es ou non,
´emanant des ´etablissements d’enseignement et de
recherche fran¸cais ou ´etrangers, des laboratoires
publics ou priv´es.

D´epartement de formation doctorale en informatique ´ Ecole doctorale IAEM Lorraine
UFR STMIA
Tˆaches de raisonnement en logiques
hybrides
TH` ESE
pr´esent´ee et soutenue publiquement le 13 d´ecembre 2010
pour l’obtention du
Doctorat de l’universit´e Henri Poincar´e – Nancy 1
(sp´ecialit´e informatique)
par
Guillaume Hoffmann
Composition du jury
Rapporteurs : St´ephane DEMRI Directeur de Recherche CNRS, ENS Cachan, France
Gert SMOLKA Professeur, Saarland University, Sarrebruck, Allemagne
Examinateurs : Patrick BLACKBURN Directeur de Recherche INRIA, Nancy, France
Claude GODART Professeur, Universit´e de Lorraine, Nancy, France
Andreas HERZIG Directeur de Recherche CNRS, IRIT, Toulouse, France
Laboratoire Lorrain de Recherche en Informatique et ses Applications — UMR 7503

R´ esum ´ e : T ˆ aches de raisonnement en logiques hybrides
Les logiques modales sont des logiques permettant la repr´ esentation et l’inf´ erence
de connaissances. La logique hybride est une extension de la logique modale
de base contenant des nominaux, permettant de faire r´ ef´ erence ` a un unique in-
dividu ou monde du mod` ele. Dans cette th` ese nous pr´ esentons plusieurs algo-
rithmes de tableaux pour logiques hybrides expressives. Nous pr´ esentons aussi une
impl´ ementation de ces calculs, et nous d´ ecrivons les tests de correction et de per-
formance que nous avons effectu´ es, ainsi que les outils les permettant. De plus, nous
´
etudions en d´ etail une famille particuli` ere de logiques li´ ee aux logiques hybrides : les
logiques avec op´ erateurs de comptage. Nous ´ etudions la complexit´ e et la d´ ecidabilit´ e
de certains de ces langages.
Mots-cl ´ es : D´ eduction automatique, tableaux, logique modale, logique hybride,
analyse en complexit´ e, terminaison, benchmarks
Abstract: Reasoning Tasks for Hybrid Logics
Modal logics are logics enabling representing and infering knowledge. Hybrid
logic is an extension of the basic modal logic that contains nominals which enable
to refer to a single individual or world of the model. In this thesis, we present sev-
eral tableaux-based algorithms for expressive hybrid logics. We also present an im-
plementation of these calculi and we describe correctness and performance tests we
carried out, and the tools that enable these. Moreover, we study a particular family of
logics related to hybrid logics: logics with counting operators. We investigate previ-
ous results, and study the complexity and decidability of certain of these languages.
Keywords: Automated deduction, tableaux, modal logic, hybrid logic, complexity
analysis, termination, benchmarks
3

4