DS4 – Pb1 – Correction de l`œil orrection de l`œil orrection de l`œil

DS4
DS4 DS4
DS4 –
––
– P
PP
Pb1
b1 b1
b1 –
––
– C
CC
Correction de l’œil
orrection de l’œil orrection de l’œil
orrection de l’œil –
––
– Lunette
Lunette Lunette
Lunette ou
ouou
ou Lentille de Contact
Lentille de Contact Lentille de Contact
Lentille de Contact
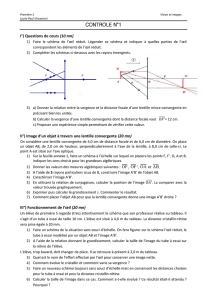
On étudie dans ce problème quelques caractéristiques des yeux, ainsi que les corrections à
apporter pour des yeux myopes. On rappelle la constitution d’un œil sur le schéma suivant. On
considérera qu’il est équivalent à une lentille mince sphérique L, de distance focale image f ’
variable et de centre O, placé à une distance d = 15mm constante de la rétine (joue le rôle d’écran
plan E) :
1. On considère un œil « normal », dont le PR (Punctum Remotum) est à l’infini, et le PP
(Punctum Proximum) est égal à 25cm.
1.a. Rappeler en quoi consistent les conditions de Gauss, et ce que cela implique sur les
lentilles minces sphériques. Comment fait-on dans la pratique pour les respecter ?
1.b. Dans le cas où l’œil n’accommode pas (mise au point sur le PR), déterminer la vergence
du cristallin correspondante. Faire un schéma.
1.c. Dans le cas où l’œil accommode au maximum (mise au point sur le PP), déterminer la
vergence du cristallin correspondante. Faire un schéma.
1.d. En vieillissant, l’œil perd de son pouvoir d’accommodation. Si le PR n’est pas modifié,
la vergence du cristallin ne peut varier que de 4,5δ à 33 ans, 1δ à 45 ans et 0,25δ à 70
ans. En déduire les PP correspondants à chacun, ainsi que l’âge d’un œil « normal ».
1.e. Prenons l’exemple d’un œil complètement fatigué, qui reste en permanence avec une
mise au point à l’infini (presbyte). Quel type de lunette faut-il placer devant l’œil pour
qu’il puisse voir nettement un objet situé à la distance D = 25cm ? Donner la distance
focale image des verres en supposant que les lunettes sont à 1 cm de l’œil. Faire un
schéma illustrant cette situation pour un objet sur l’axe optique.
2. On considère maintenant une personne très myope, dont le PR est de 11 cm au lieu de
l’infini. On souhaite corriger sa vue pour ramener le PR à l’infini.
2.a. Un opticien lui propose une paire de lunettes, dont chaque verre est modélisé par une
lentille mince sphérique de centre O L et de distance focale image f L ’ située à la
distance =
1
L
O O cm
de l’œil. Préciser les caractéristiques de ces verres. Faire un
schéma représentant l’image sur la rétine d’un objet AB transverse venant de l’infini.
2.b. Après réflexion, la personne opte pour des verres de contact, c'est-à-dire des lentilles
minces sphériques qui sont directement accolées à l’œil (on pourra supposer la
distance nulle). Qu’est-ce que cela change pour les caractéristiques des verres ?
Cristallin
Rétine
d
O
E

DS4
DS4 DS4
DS4 –
––
– P
PP
Pb
bb
b2
22
2 :
: :
: Grossissement d’une Lunette Astronomique
Grossissement d’une Lunette AstronomiqueGrossissement d’une Lunette Astronomique
Grossissement d’une Lunette Astronomique
On considère une lunette astronomique formée :
- d’un objectif constitué d’une lentille mince convergente L 1 de distance focale
1 1 1
' ' 0
f O F
= >
- d’un oculaire constitué d’une lentille mince convergente L 2 de distance focale
2 2 2
' ' 0
f O F
= >
Ces deux lentilles ont même axe optique ∆.
On rappelle qu’un oeil normal voit un objet sans accommoder quand celui-ci est placé à l’infini.
On souhaite observer la planète Mars, qui est vue à l'oeil nu sous un diamètre apparent α.
1. Pour voir la planète nette à travers la lunette, on forme un système afocal.
a. Que cela signifie-t-il ? Que cela implique-t-il pour les positions des lentilles ?
b. Faire le schéma de la lunette en prenant
1 2
' 5 '
f f
=
Dessiner sur ce schéma la marche à travers la lunette d’un faisceau lumineux formé
de rayons issus de l’étoile. On appellera
' '
A B
, l’image intermédiaire.
c. On souhaite photographier cette planète. Où faut-il placer la pellicule (sans rajouter
de dispositif supplémentaire) ?
2. On note α’, l’angle que forment les rayons émergents extrêmes en sortie de la lunette.
a. L’image est-elle droite ou renversée (justifier) ?
b. La lunette est caractérisée par son grossissement
'
G
α
α
= . Exprimer G en fonction de
1
'
f
et
2
'
f
.
c. Le principal défaut d’une lentille est appelé défaut d’aberrations chromatiques :
expliquer brièvement l’origine de ce défaut et ses conséquences. Pour quelle raison
un miroir parfait n’a-t-il pas ce défaut ?
3. On veut augmenter le grossissement de cette lunette et redresser l’image. Pour cela, on
interpose entre L 1 et L 2 , une lentille convergente L 3 de distance focale
3 3 3
' ' 0
f O F
= >
.
L’oculaire L 2 est déplacé pour avoir de la planète une image nette à l’infini à travers le
nouvel ensemble optique.
a. Quel couple de points doit conjuguer L 3 ? Compléter le schéma suivant :
b. On appelle
3
γ
, le grandissement de la lentille 3. En déduire
3 1
'
O F
en fonction de
3
'
f
et de
3
γ
.
c. Faire un schéma. (On placera O
3
entre
1
'
F
et
2
F
et on appellera
' '
A B
la première
image intermédiaire et
'' ''
A B
, la seconde image intermédiaire).
d. En déduire le nouveau grossissement G' en fonction de
3
γ
et de G. Comparer à G, en
norme et en signe.
L
1
L
3
∞
A
?
L
2
? ?

DS4 – Pb3 : Appareil Photographique – Etude d’un Téléobjectif
(Extrait des Petites Mines 2009)
Un téléobjectif est un objectif de longue focale, c’est-à-dire un objectif dont la focale est
supérieure à la diagonale de la pellicule pour un appareil photographique argentique ou de la matrice de
cellules photosensibles dans le cas d’un appareil photographique numérique. Ces objectifs permettent
un cadrage serré des sujets photographiés grâce à un angle de champ étroit.
On considère dans ce problème que le sujet photographié est constitué par la tour Eiffel culminant à
une hauteur h = 324 m du sol et située à une distance d = 2,0 km du photographe.
Partie 1 : Objectif standard
Partie 1 : Objectif standard Partie 1 : Objectif standard
Partie 1 : Objectif standard
On s’intéresse dans un premier temps à un objectif standard d’appareil photographique
argentique constitué d’une lentille convergente unique de centre O et de focale f ’ = 50 mm.
Q1.
Q1. Q1.
Q1. Quelle doit être la distance D entre la lentille et la pellicule pour que la photographie soit
nette ? Justifier votre réponse.
Q2.
Q2. Q2.
Q2. Construire sur un schéma l’image de l’objet sur la pellicule (sans respecter l’échelle).
Q3.
Q3. Q3.
Q3. On appelle h 1 la hauteur de l’image de la tour Eiffel sur la pellicule. Déterminer son expression
en fonction de f ’, d et h puis calculer sa valeur numérique.
Partie
Partie Partie
Partie 2 : Réalisation d’un t
2 : Réalisation d’un t2 : Réalisation d’un t
2 : Réalisation d’un téléobjectif avec une lentille unique
éléobjectif avec une lentille unique éléobjectif avec une lentille unique
éléobjectif avec une lentille unique
Q4.
Q4. Q4.
Q4. Expliquer pourquoi, si l’on souhaite photographier les détails d’un sujet lointain, il faut choisir
un objectif de focale plus élevée que celle d’un objectif standard.
Q5.
Q5. Q5.
Q5. Dans le cas d’un téléobjectif de focale
0
' 200
f mm
= , calculer la hauteur h 2 de l’image de la
tour Eiffel sur la pellicule ainsi que l’encombrement de l’appareil (distance entre la lentille et
la pellicule)
Q6.
Q6. Q6.
Q6. La matrice de cellules photosensibles de la plupart des reflex numériques est plus petite que la
surface impressionnable de la pellicule d'un reflex 24x36. Justifier alors pourquoi un
téléobjectif de focale donnée permet un cadrage plus serré du sujet avec un appareil
numérique qu’avec un appareil argentique.
On considère dans un premier temps une lentille de
verre d’indice n placée dans l’air (figure ci-contre). On se
place dans l’approximation d’un indice n ne dépendant pas
de la longueur d’onde.
Q7.
Q7. Q7.
Q7. Reproduire la figure ci-dessus et tracer la marche du rayon incident représenté dans et après la
lentille. Justifier sommairement le tracé.
Q8.
Q8. Q8.
Q8. Quelle est la nature de cette lentille ? Justifier.
Q9.
Q9. Q9.
Q9. Définir le foyer image d’un système optique. Indiquer sur votre schéma la position du foyer
image F’ de la lentille.

L’indice de réfraction n du verre constituant la lentille dépend en réalité de la longueur d’onde λ
de la radiation lumineuse qui la traverse. Ils sont reliés par la loi de Cauchy :
( )
2
b
n aλ
λ
= + , où a et
b sont des constantes positives qui ne dépendent que du milieu traversé.
Q10.
Q10. Q10.
Q10. Comparer r R et r B , angles réfractés en sortie de lentille pour une radiation rouge et pour une
radiation bleue en considérant des rayons incidents parallèles à l’axe optique. Tracer alors les
chemins suivis par ces deux radiations dans et après la lentille.
Q11.
Q11. Q11.
Q11. Expliquer le problème qui pourrait se poser si l’on réalisait un téléobjectif avec une lentille
unique. Comment s’appelle ce phénomène ?
On peut s’affranchir de ce problème en réalisant un doublet, équivalent à une lentille convergente
unique, constitué d'une lentille convergente accolée à une lentille divergente, les deux lentilles étant
taillées dans des verres d’indices de réfraction différents. Le téléobjectif ainsi constitué présente
toutefois l’inconvénient d’un encombrement important.
Partie
Partie Partie
Partie 3 : Réalisation d’un téléobjectif par association de deux lentilles distantes de e
3 : Réalisation d’un téléobjectif par association de deux lentilles distantes de e 3 : Réalisation d’un téléobjectif par association de deux lentilles distantes de e
3 : Réalisation d’un téléobjectif par association de deux lentilles distantes de e
Afin de raccourcir les téléobjectifs, en particulier les plus puissants, on peut réaliser un autre
montage en associant deux lentilles distantes d’une distance e : une lentille convergente L 1 de centre
O 1 et de focale
1
'
f
et une lentille divergente L 2 de centre O 2 et de focale
2
'
f
.
On prendra pour les applications numériques :
1
' 50
f mm
= ,
2
' 25
f mm
= − et e = O 1 O 2 = 31 mm.
On note P l’intersection du plan de la pellicule avec l’axe optique et F’ l’image par le téléobjectif d’un
point à l’infini sur l’axe optique.
Q12.
Q12. Q12.
Q12. Déterminer littéralement la position de F’ en fonction de
1
'
f
,
2
'
f
et e. En déduire
l’expression de l’encombrement O 1 P de l’appareil en fonction de ces mêmes grandeurs. Après
l’avoir calculé approximativement, déterminer laquelle de ces trois valeurs : O 1 P = 14 cm,
O 1 P = 11 cm et O 1 P = 8,0 cm correspond à l’encombrement du téléobjectif.
Q13.
Q13. Q13.
Q13. Déterminer l’expression de h 3 , hauteur de l’image de la tour Eiffel sur la pellicule en fonction
de
1
'
f
,
2
'
f
, e, d et h. Après l’avoir calculée approximativement, déterminer laquelle de ces
trois valeurs : h 3 = 14 mm, h 3 = 34 mm et h 3 = 54 mm correspond à la hauteur de l’image sur la
pellicule.
Q14.
Q14. Q14.
Q14. Commenter les résultats précédents.