Énoncé - Physique

DS6 : Mécanique
Durée 4h, calculatrices autorisées. Le DS est probablement trop long pour que vous puissiez tout faire, c’est normal, faites-en le
maximum.
Exercice 1
(R)
(Oz)
O
x
z
x0
z0
A
Ap
i
G
p
A
i
G m=,·
~
P
~
Fm
~
Fp
~
Ft
Fp=1
2ρSv2Cp
Ft=1
2ρSv2Ct
ρ=, −
S= v
g=, −
Cp Ct i (i=)
Cp=, Ct=,
η
η
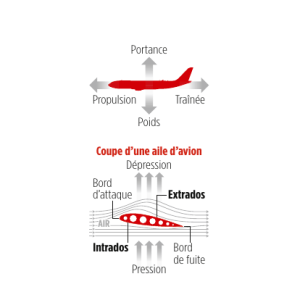
I – Vol en montée
p
i= 0 Pm
~
P~
Fm~
Fp ~
Ft
~
P+~
Fm+~
Fp+~
Ft=~
0
Ox0 Oz0
v A
v=s2mg A
ρSCp

~
Fm k~
Fmk v
A Pm
Pm=Pm0( A+f0 A)√ A f0=Cp
Ct
Pm0=mg Ct
Cps2mg
ρSCp
Pm0 f0 Pm0
Pm=P =
Pm
A x1 x≈x x≈1
vz A
η A
II – Vol en virage
R p= i=
v φ φ
Φ
~
P+~
Fm+~
Fp+~
Ft=−mv2
R~ur
~ur
~ur ~uz R
v φ g
η φ
η
Exercice 2
(AB) (BC) (CD) (EF )
A
B C
D E F
(AB) α=
β=
~
F1
α β
B , −
F2=
x(t)
v(t) x(t)
(CD) α0= F3
F3=kv2 k=, −
vl

vl vl
(EF ) γ=
F −
x(t) y(t)
x(t) y(t) F
F
Données
h=, m= AB = g=, −
Exercice 3
R J∆=MR2 M
m
R
θ0
∆
J∆ω
θ0
L∆ ω
t= 0 dω
dt Rθ0m
J∆
ω(t)
Ec(t)
v0= /
R= m= θ0= M=
θ0= 0
∆ Γ∆
dω
dt
dω
dt =mRg θ0−Γ∆
J∆
θ0
Comment faire subir un looping au Hamster ?
v0 θ0= 0
ω0

ω1
ω1=ω0sJ∆
J∆+mR2
ω θ
ω θ
π
~a =−Rω2
1−2mgR(1 − θ)
J∆+mR2~er
Exercice 4
J∆
r S m
t= 0
h(t) θ(t)
h(t) θ(t)
m
¨
h(t) T
¨
θ(t)
T
α=
¨
θ(t)
a=¨
h(t) S
J∆=, r= m= α a
h
~e∆
r
θ(t)
M
m
z
h
0
1
/
4
100%