2012

!
1!
CONCOURS D'ADMISSION à L'ECOLE D'ORTHOPTIE DE
RENNES
SESSION 2012
ÉPREUVE DE PHYSIQUE
Durée : 2 heures
Ce sujet comporte 2 exercices.
L’exercice 1 est sur 10 points, l’exercice 2 est sur 10 points.
Il sera tenu compte du soin et de la rédaction.
Vous devez impérativement respecter la numérotation des questions.
Exercice 1 : Le sondeur à ultrasons (10 points)
Sur un bateau, un sondeur est un appareil servant à mesurer la profondeur de
la mer (la distance entre la surface et le fond de la mer). Les sondeurs sont
généralement acoustiques : la profondeur est déduite de la mesure du temps
de trajet d’un signal acoustique réfléchi par le fond. Le signal acoustique
utilisé est une onde ultrasonore.
Quelques généralités sur les ondes :
1. Définir ce qu’est une onde mécanique.
2. Les ultrasons sont-ils des ondes mécaniques ? Si oui, donner un
exemple d’onde non-mécanique, si non à quel type d’ondes
appartiennent les ultrasons ?
3. L’onde ultrasonore est-elle une onde longitudinale ou transversale ?
Justifier la réponse.
4. Citer un fait expérimental qui permet de décrire les ultrasons comme
une onde.
Étude des ultrasons émis:
Le sondeur émet des salves
d’ultrasons à intervalles de
temps régulier. On étudie
une salve d’ultrasons grâce
à l’oscillogramme ci-contre,
obtenu à partir d’un capteur
délivrant un signal lié aux
ultrasons. Le coefficient de
balayage est de 10 µs par
division.
EXERCICE III. CÉRAMIQUES ET ULTRASONS (4 POINTS)
National 2006
Les ultrasons sont utilisés dans de nombreux domaines de la vie courante : échographie, détecteurs
de présence dans les alarmes, etc. Les émetteurs et les récepteurs d'ultrasons sont fréquemment
constitués de céramiques piézoélectriques.
Les parties 1 et 2 de cet exercice sont indépendantes.
1. Émission et propagation de l'onde ultrasonore produite par une céramique piézoélectrique
Lorsqu'on applique une tension sinusoïdale d'amplitude suffisante et de fréquence appropriée entre
les deux faces métallisées et opposées d'une céramique piézoélectrique, elle se met à vibrer.
Lorsque la céramique entre en résonance elle émet des ultrasons.
La fréquence des ultrasons émis est égale à la fréquence de vibration de la céramique émettrice.
1.1. Propagation des ondes ultrasonores
On réalise le montage schématisé figure 7. Le récepteur, constitué d'une céramique réceptrice, est
placé à une distance d, face à la céramique émettrice.
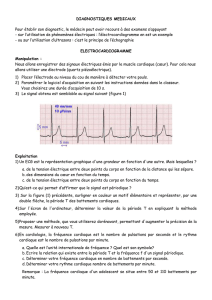
Une tension de même fréquence que les ultrasons reçus apparaît aux bornes de la céramique
réceptrice. On visualise cette tension sur la voie A d'un oscilloscope. L'oscillogramme obtenu est
représenté sur la figure 8. Le coefficient de balayage est égal à 10 µs / div et la sensibilité verticale à
0,2 V / div.
On rappelle que la célérité des ultrasons dans l'air est vair = 340 m.s – 1 dans les conditions de
l'expérience.
1.1.1. Déterminer la période T et la fréquence f de la tension observée à l'oscilloscope.
1.1.2. En déduire la fréquence fu des ultrasons. Justifier.
1.1.3. Donner l'expression littérale puis la valeur de la longueur d'onde ! des ultrasons dans
l'air.
Figure 8 :
Fi
g
ure 7 :
Émetteur Récepteur
dVoie A

!
2!
5. Déterminer la fréquence des ultrasons utilisés.
6. La célérité des ultrasons dans l’eau de mer est v = 1,5 km.s-1. En
déduire la longueur d’onde des ultrasons utilisés.
7. On suppose que l’eau n’est pas un milieu dispersif pour les ultrasons.
Définir ce qu’est un milieu dispersif. En déduire la valeur de la célérité
des sons dans l’eau de mer.
8. Entre l’émission de la salve d’ultrasons vers le fond marin et sa
réception par le sondeur après réflexion sur le fond, il s’est écoulé une
durée Δt = 32 ms. Quelle est la profondeur de la mer ?
Étude du circuit d’émission des ultrasons :
Pour que le sondeur émette des ultrasons à la bonne fréquence, il faut
un circuit qui génère une tension sinusoïdale de même fréquence que
les ultrasons. Un tel circuit peut-être un circuit RLC série :
9. Établir l’équation différentielle en uC de ce circuit.
10. On se place dans le cas d’un amortissement négligeable : R = 0. On
suppose qu’à t = 0, le condensateur est chargé sous une tension U0.
10.1. Effectuer la résolution analytique de l’équation différentielle pour
la tension uC.
10.2. En déduire l’expression de l’intensité dans le circuit.
10.3. La bobine a pour inductance L = 12 mH. Quelle valeur de
capacité du condensateur doit-on choisir ?
11. En réalité la résistance R n’est jamais nulle. On la supposera assez
faible pour que des oscillations soient toujours réalisables dans le
circuit.
11.1. De quel type de régime de fonctionnement du circuit RLC s’agit-
il ?
11.2. Dans le cas d’amortissements faibles tracer l’allure (sans aucun
soucis d’échelle) de la courbe représentant uC au cours du
temps.
11.3. Expliquer en termes énergétiques les échanges énergétiques
qui ont lieu lors de la première pseudo-période.
1.2. Résonance de la céramique émettrice
Pour une valeur appropriée de la fréquence de la tension sinusoïdale appliquée, son amplitude
restant constante, la céramique émettrice entre en résonance. La tension sinusoïdale joue alors le
rôle d'un excitateur et la céramique celui d'un résonateur.
1.2.1. Que peut-on dire de la valeur de la fréquence de la tension excitatrice à la résonance ?
1.2.2. Décrire qualitativement le phénomène de résonance en ce qui concerne l'amplitude de
vibration de la céramique.
2. Oscillations libres dans un circuit RLC série
Pour étudier les conditions d'obtention d'oscillations électriques libres à la fréquence propre
f0 = 40 kHz, on réalise le circuit schématisé figure 9. Un oscilloscope à mémoire permet d'enregistrer
la tension aux bornes du condensateur. L'oscillogramme est représenté sur la figure 10.
La bobine a une inductance de valeur L = 1,0 mH ; R est 1a résistance totale du circuit.
Le condensateur est initialement chargé sous une tension UC = 4,0 V.
À l'instant de date t = 0 s, on ferme l'interrupteur K.
2.1. Comment appelle-t-on le type de régime correspondant à la figure 10 ?
2,2. Interpréter en termes d'énergie l'amortissement des oscillations que l'on observe.
2.3. Comment peut-on éviter l'amortissement des oscillations, sachant que la résistance du circuit ne
peut pas être nulle ?
2.4. Dire si les affirmations ci-dessous concernant les oscillations libres d'un dipôle RLC sont vraies
ou fausses. Commenter brièvement.
AFFIRMATION 1: En augmentant la résistance R d'un dipôle RLC on observera toujours des
oscillations amorties.
AFFIRMATION 2: La valeur de la période propre d'un dipôle RLC dépend de la charge initiale du
condensateur.
Figure 10 :
Figure 9 :
LR
C
iuC uL
K

!
3!
Exercice 2 : Le fluor 18 (10 points)
Le fluor 18 ( ) est utilisé comme traceur en imagerie médicale. Le fluor 18
se désintègre selon une radioactivité de type β+, sa demi-vie est de 110
minutes.
On donne un extrait du tableau périodique des éléments :
Lithium
Béryllium
Bore
Carbone
Azote
Oxygène
Fluor
Néon
La masse des noyaux et des particules peut être exprimée en unité de masse
atomique, de symbole u. La masse du noyau de fluor 18 est m1 = 17,9960 u
Rappel : 1,00 u = 1,66.10-27 kg.
La célérité de la lumière dans le vide est c = 3,00.108 m.s-1.
1. Écrire l’équation de désintégration du fluor 18. Quelle est la
composition du noyau fils obtenu et le nom de la particule émise ?
2. Dans l’extrait de la classification périodique des éléments, il n’est pas
mentionné le fluor 18 mais le fluor 19. Expliquer cette différence.
3. Donner la définition du temps de demi-vie.
4. Déterminer la valeur de la constante radioactive du fluor 18.
5. On souhaite administrer à un patient, une dose de fluor 18 dont
l’activité est A = 180 MBq. Déterminer le nombre de noyaux de fluor 18
que cela représente. Calculer, en kg, la masse de fluor
correspondante. Conclure.
6. À t = 0, on administre au patient la dose décrite à la question
précédente. Calculer l’activité due au fluor 18 au bout d’une heure.
7. Déterminer la durée nécessaire pour l’activité du fluor 18 ne soit plus
que de 1,0 % de l’activité à t = 0.
8. On souhaite calculer les valeurs de l’activité au cours du temps, par la
méthode d’Euler.
8.1. Pour cela, on choisit un pas d’itération (ou de résolution) de
100 s. La valeur est-elle compatible avec ce système ?
8.2. En prenant toujours A = 180 MBq à t = 0, déterminer par la
méthode d’Euler, l’activité à t = 100 s et t = 200 s. On détaillera
tous les calculs et la méthode suivie.
9. La masse du noyau de fluor 18 est m1 = 17,9960 u. Celle du noyau fils
est m2 =17,9948 u. Celle de la particule émise lors de la désintégration
du fluor 18 est m3 = 5,48.10-4 u.
9.1. Calculer l’énergie dégagée lors de la désintégration d’un noyau
de fluor 18.
9.2. En déduire l’énergie que reçoit le patient lors de la première
seconde de son traitement.