Polycopié d`exercices et recueil des problèmes d`examen

Universités Paris 6, Paris 7 & Paris 11 ; Observatoire de Paris –
Master 2 Recherche « Astronomie, Astrophysique & Ingénierie spatiale »
ET9
Objets compacts et phénomènes associés
Exercices et problèmes
Frédéric Daigne
(Institut d’Astrophysique de Paris, Université Pierre et Marie Curie)
Année 2015 – 2016
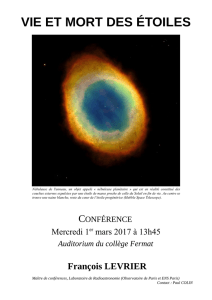
La nébuleuse du Crabe, observée par Chandra, HST et Spitzer.

La nébuleuse du Crabe. Image composite obtenue à partir d’observations en X par Chandra (bleu), dans le
visible par HST (jaune et rouge) et dans l’infrarouge par Spitzer (violet).
2

I. Introduction
1. La compacité – 2. Évolution stellaire – 3. Populations d’objets compacts
Exercice 1 : Compacité des étoiles
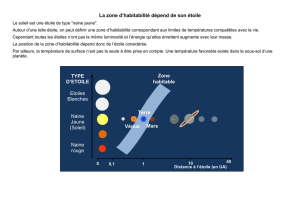
En utilisant des relations masse-rayon adaptées, évaluer l’évolution de la compacité en fonction de la masse
pour les étoiles de la séquence principale, et pour les naines blanches.
Exercice 2 : Compacité des naines blanches
Exercice 2 de l’examen 2015 (voir page 24).
Exercice 3 : Modèle à 1 zone
Construire le modèle à 1 zone des étoiles de la séquence principal proposé dans le chapitre 2 du cours est
un excellent entraînement pour manier les concepts élémentaires sur la structure hydrostatique, le transport
radiatif et le rayonnement thermique des étoiles.
Exercice 4 : Rotation maximale d’une étoile
On considère une étoile de masse M, en rotation autour d’un axe. Son rayon à l’équateur est R.
1. En faisant le bilan des forces qui s’appliquent sur un élément de masse dm à l’équateur, expliquer pour-
quoi il existe une vitesse de rotation maximale au-delà de laquelle l’étoile ne peut plus être en équilibre
hydrostatique. Que se passe-t-il alors ?
2. Montrer que la vitesse de rotation maximale est approximativement égale à la vitesse de rotation képle-
rienne à l’équateur.
3. Montrer que la période de rotation minimum (correspondant à cette vitesse de rotation maximale) ne
dépend que de la masse volumique moyenne de l’étoile.
4. Représenter cette période minimum en fonction de la masse volumique moyenne et placer approximative-
ment sur ce diagramme le Soleil, une naine blanche et une étoile à neutrons.
Exercice 5 : Echelles de temps de gravitationnelles et nucléaires
Ecrire le rapport de l’échelle de temps de Kelvin-Helmholtz sur l’échelle de temps nucléaire en faisant ap-
paraître la compacité de l’étoile. Montrer que le rapport obtenu est un rapport entre deux efficacités à définir.
Discuter les conséquences du résultat pour l’évolution stellaire.
Exercice 6 : Efficacités comparées de processus d’extraction de l’énergie
On considère une étoile de masse M, de compacité Ξ∗et de vitesse angulaire Ω∗qui s’effondre gravitation-
nellement (sans perte de masse) en un astre plus petit de compacité Ξ = GM/Rc2.
1. Evaluer la vitesse angulaire Ωde l’astre final. L’exprimer le rapport Ω/Ωcr, où Ωcr est la vitesse angulaire
critique définie dans l’exercice « Rotation maximale d’une étoile », en fonction du rapport initial Ω∗/Ωcr,∗.
2. Proposer un ordre de grandeur raisonnable pour Ξ∗et Ω∗/Ωcr,∗.
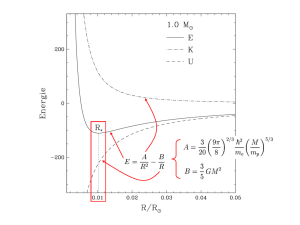
3. Représenter en fonction de la compacité Ξles énergies suivantes : (a) l’énergie que l’étoile initiale libère
au cours de son existence par fusion nucléaire (on ne considèrera que la fusion de l’hydrogène pendant
la séquence principale) ; (b) l’énergie gravitationnelle libérée par l’effondrement gravitationnel de l’étoile
initiale produisant le nouvel astre plus compact ; (c) l’énergie de rotation du nouvel astre.
4. Ordonner les différents processus d’extraction de l’énergie du plus au moins efficace en fonction de la
compacité et discuter la position dans le diagramme des différentes classes d’objets compacts de masse
stellaire.
Exercice 7 : Novae et sursauts X (début)
Problème d’examen 2010 : questions 1. à 5. (voir page 8).
Exercice 8 : Sursaut X
Exercice 2 de l’examen 2015 (voir page 24).
3

Exercice 9 : Trous noirs supermassifs (début)
Exercice 2 de l’examen 2013 jusqu’à la question 15. (voir page 17).
Exercice 10 : Candidat trou noir de masse intermédiaire
Exercice 1 de l’examen 2014 (voir page 20).
II. Les objets compacts ? Leur émission lorsqu’ils sont isolés
4. Naines blanches – 5. Étoiles à neutrons – Pulsars – 6. Trous noirs
Exercice 11 : Naine blanche magnétisée en rotation Exercice de l’examen 2010 (page 8).
Exercice 12 : Dissipation du champ magnétique d’une étoile à neutrons
L’intérieur d’une étoile à neutrons est supraconducteur. L’ordre de grandeur caractéristique de la résistivité
électrique ηest très petit et peut s’obtenir simplement par analyse dimensionnelle à partir des constantes
fondamentales e,me,0et c. En déduire une échelle de temps caractéristique pour la dissipation magnétique
d’un pulsar. Faire l’application numérique pour le pulsar du Crabe et conclure.
(pour cet exercice, il peut être utile de consulter l’annexe F. et en particulier les paragraphes F.4 et F.5)
Exercice 13 : Loi de décélération d’un pulsar dominé par l’émission d’ondes gravitationnelles
En raison de sa rotation rapide, une étoile à neutrons en rotation s’aplatit et possède donc un rapport
= (a−b)/((a+b)/2) plus petit que 1, où aet bsont les valeurs supérieure et inférieure du rayon de l’étoile
déformée. Cet écart à la symétrie sphérique conduit à un mécanisme de ralentissement du pulsar par émission
d’onde gravitationnelle, selon la loi (quadrupôle d’Einstein) :
˙
EGW =−32
5
G
c5I22Ω6.
Ecrire la loi de décélération d’un pulsar pour lequel se processus serait dominant, et l’échelle de temps corres-
pondante. Faire l’application numérique pour le pulsar du Crabe en prenant ∼3×10−4et comparer aux
valeurs obtenues dans le modèle du dipôle magnétique pour ce même pulsar, et à l’âge connu du pulsar du
Crabe. Conclure.
(en prolongement, on peut étudier l’évolution d’un pulsar qui émet à la fois un rayonnement électromagnétique
et des ondes gravitationnelles, et discuter le mode dominant dans chaque phase mise en évidence)
Exercice 14 : Potentiel de Paczynski-Wiita.
Ces deux auteurs ont proposé dans un article de 1980 de « mimer » les effets de la relativité générale
en gravité newtonienne en utilisant pour le potentiel gravitationnel d’un trou noir sans rotation l’expression
suivante :
Φ(r) = −GM
r−RS
,
où RSest le rayon de Schwarzschild. Ce potentiel est parfois utilisé dans certains modèles de trous noirs ac-
crétants lorsque la prise en compte de la relativité générale n’est pas possible. Calculer le moment angulaire
spécifique d’une particule sur une orbite circulaire autour du trou noir et montrer qu’il existe une dernière orbite
stable au rayon prévu par la relativité générale.
Exercice 15 : Evaporation d’un trou noir.
Calculer le temps mis par un trou noir pour s’évaporer du fait de son rayonnement thermique (rayonnement
de Hawking). Faire l’application numérique pour un micro-trou noir primordial (M < 1012 kg), un trou noir
stellaire et un trou noir supermassif. Conclure.
Exercice 16 : Novae et sursauts X (début)
Problème d’examen 2010 : questions 6. à 12. (voir page 8).
4

Exercice 17 : Destruction d’une naine blanche par effet de marée
Exercice 1 de l’examen 2013 (voir page 17).
Exercice 18 : La supernova SN 2014J dans la galaxie proche M82 (début)
Exercice II de l’examen 2014 (voir page 20) : début du 2.1, début du 2.2.
Exercice 19 : Pulsars
Exercice 4 de l’examen 2015 (voir page ??).
Exercice 20 : Pulsar milliseconde
Exercice 1 de l’examen 2012 (voir page 14).
Exercice 21 : Glitches des pulsars (difficile).
Cet exercice discute grossièrement l’interprétation ancienne qui était faite des glitches des pulsars, à savoir
des tremblements de croûte. Aujourd’hui, cette interprétation est abandonnée au profit d’un mécanisme plus
complexe faisant intervenir la structure interne.
On modélise une étoile à neutrons par une croûte solide et un cœur de neutrons superfluide. On note Ωc(t)
et Ic,Ωn(t)et Inla vitesse angulaire et le moment d’inertie respectivement de la croûte et du cœur. Si une
perturbation (« tremblement de croûte ») a lieu dans la croûte, elle se transmet dans le reste de l’étoile à cause
du champ magnétique ancré dans la surface de l’étoile. Par exemple, si un morceau « ralentit », cela va perturber
les lignes de champ magnétique à cet endroit et la perturbation se propage. L’échelle de temps correspondante
donne une estimation du temps nécessaire à la croûte pour réagir à la perturbation.
1. Par analogie avec la vitesse du son, écrire la vitesse de propagation d’une perturbation magnétique en
remplaçant la pression par la pression magnétique (vitesse d’Alfven vA).
2. En prenant le rayon de l’étoile à neutrons comme taille caractéristique, déterminer l’échelle de temps tA
correspondante. Ordre de grandeur pour le pulsar du Crabe ?
3. La réponse du cœur superfluide est plus lente car la superfluidité diminue le couplage avec la croûte. On
modélise les évolutions des vitesses angulaires en l’absence de perturbation de la manière suivante :
Ic˙ Ωc=−α−Ic
Ωc−Ωn
τc
,(1)
In˙ Ωn= +Ic
Ωc−Ωn
τc
.(2)
Pouvez-vous interpréter chaque terme ? Que représentent αet τc?
4. Trouver la solution de ce système (combien de constantes d’intégration ?). On pourra poser I=Ic+Inet
τ=In
Iτc.
5. Déterminer le régime stationnaire (t/τ →+∞). Application numérique : si Ic∼Incomme suggéré par
les E.O.S. réalistes, quelles est la différence relative de vitesse angulaire entre le cœur et la croûte ? (on
prendra les paramètres du Crabe donnés dans le cours pour évaluer les constantes nécessaires).
6. Pour modéliser un « glitch », on suppose qu’à t= 0, on perturbe le régime stationnaire Ωstat
c(t)et Ωstat n(t)
avec Ωc→Ωc(0) + ∆Ωc,0. Montrer que l’évolution de la vitesse angulaire de la croûte peut se mettre sous
la forme
Ωc(t)=Ωstat
c(t) + ∆Ωc,0Qe−tτ + 1 −A.
Le paramètre Qs’appelle « paramètre de guérison ». Tracer l’allure de Ωc(t)pour différentes valeurs de
0≤Q≤1.
7. Comment peut-on mesurer τet Qen observant un « glitch » ?
8. Pourquoi la mesure de Qnous donne-t-elle une information sur la structure interne de l’étoile à neutrons ?
Exercice 22 : Refroidissement d’une naine blanche (très difficile)
On rappelle que les naines blanches ont une masse typique ∼1M, un rayon de quelques 103km et une
masse volumique moyenne ∼109kg.m−3. Leur température interne est inférieure à 107K. Pour une naine
blanche d’hélium, la masse molaire moyenne par électron est µe= 2.
Dans une naine blanche, les réactions nucléaires sont arrêtées et les pertes neutrinos négligeables (ceci n’est
pas strictement valide au tout début de son évolution). La naine blanche peut être considérée en très bonne
5