Les angles : vocabulaires et propriétés

Les angles : vocabulaires et propriétés
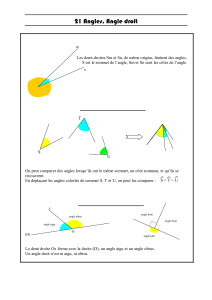
Ci-contre est représenté l’angle a AOB :
• Le point O est le sommet de l’angle.
• Les demi-droites [OA) et [OB) sont les côtés de l’angle.
L’unité usuelle de mesure des angles est le degré, noté « ° »
L’instrument de mesure des angles est le rapporteur.
Angle nul Angle aigu Angle droit Angle obtus Angle plat
Sa mesure est de
zéro degré.
Sa mesure est
comprise entre 0°
et 90°
Sa mesure est de
90°.
Sa mesure est
comprise entre
90° et 180°.
Sa mesure est de
180°
Utilisation du rapporteur :
• Le centre du rapporteur doit être sur le sommet de l’angle.
• Un zéro du rapporteur doit être sur un côté de l’angle.
• Lire la graduation qui correspond en partant de ce zéro.
L’an
g
le a YAZ mesure 125°, c’est un an
g
le obtus.
L’an
g
le a XAY mesure 55°, c’est un an
g
le ai
g
u.
Deux angles adjacents Deux angles complémentaires Deux angles supplémentaires
Ils ont le même
sommet, un côté en
commun et ils sont de
part et d’autre de ce
côté commun.
La somme de leur mesure vaut
90°.
La somme de leur mesure vaut
180°.
Remarque : Deux angles complémentaires ou supplémentaires ne sont pas
forcément adjacents.
a
xOy et a yOz sont
adjacents.
Exemple, les deux angles aigus
du triangle rectangle sont
complémentaires.
Exemple, les deux angles
consécutifs d’un parallélogramme
sont supplémentaires.
d
J + d K = 180°
d
E + d F = 90°

Les angles : vocabulaires et propriétés (suite)
Définition : Deux angles opposés par leur sommet sont deux angles symétriques par rapport
à leur sommet.
Propriété :
Si deux angles sont opposés par leur sommet alors ils sont de même mesure.
a
XOY et a UOV sont opposés par le sommet.
Ces deux angles sont de même mesure
Définition :
Soient deux droites (d) et (d’) coupées par une sécante,
dire que deux angles sont alternes-internes signifie
que :
• Ils n’ont pas le même sommet.
• Ils sont de part et d’autre de la sécante.
• Ils sont à l’intérieur de la partie délimitée par les
droites (d) et (d’).
Exemple : les deux angles
marqués sont alternes-internes.
Définition :
Soient deux droites (d) et (d’) coupées par une sécante,
dire que deux angles sont correspondants signifie que :
• Ils n’ont pas le même sommet.
• Ils sont du même côté de la sécante.
• L’un est à l’intérieur de la partie délimitée par les
droites (d) et (d’), l’autre est à l’extérieur.
Exemple : les deux angles
marqués sont correspondants.
Propriété :
Si les droites (d) et (d’) sont parallèles alors :
• Les angles alternes-internes déterminés par une sécante sont de même mesure.
• Les angles correspondants déterminés par une sécante sont de même mesure.
Réciproquement :
Si deux angles alternes-internes (ou correspondants) déterminés par deux droites et une
sécante sont de même mesure alors les deux droites sont parallèles.
(d) et (d’) sont parallèles.
En rouge, deux angles correspondants.
En vert, deux angles alternes-internes.