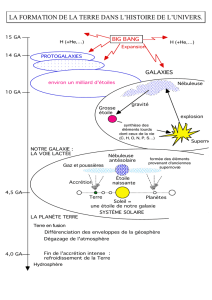
DL8-2 dynamique stellaire et galactique _centrale TSI 1999

MP – Physique-chimie. Devoir surveillé
Jean Le Hir, 19 mars 2008 Page 1 sur 4
DL n°8-2 : corrigé
Mécanique du point.
Exemples de dynamique stellaire et galactique
I.A. Préliminaire
I.A.1) Expression de la force gravitationnelle :
2
S
r
M m
f G e
r
= −
Dimension de G :
[ ] [ ]
[
]
[ ] [ ][ ][ ]
[
]
[ ] [ ] [ ] [ ]
2 2
2 1 3 2
2 2
L L
G F M L T M L T
M M
− − −
= = = . L’unité dans le système
international est donc le mètre cube par kilogramme et par seconde au carré :
3 1 2
m kg s
− −
⋅ ⋅
I.A.2) Troisième loi de Kepler. Dans le cas d’un mouvement circulaire, l’accélération est connue :
22
2
r
d d
a R e R e
dt dt
θ
θ θ
= − +
Le fait que l’accélération soit centrale (pas de composante de force selon
e
θ
) implique que le
mouvement est uniforme : 2
te
d
C
dt T
θ π
= ω= = .
L’accélération centrale a donc pour module
2
2
2 2
4
S
r
M
R f
a R G
T m R
π
= ω = = =
Cette dernière expression correspond à la troisième loi de Kepler exprimée dans le cas particulier des
orbites circulaires :
3
2 2
4
S
GM
R
T
=
π
I.B. Application
I.B.1) Estimation grossière de la masse de la Galaxie. En appliquant la troisième loi de Kepler, nous
obtenons cet ordre de grandeur :
2 3 41 11
int 2
4
3 10 kg 1,5 10
S
S
D
M M M
G T
π
> = ≈ × ≈ ×
I.B.2) Comparer à la valeur
11
6 10
S
M
M= × déterminée par les astronomes.
Tout d’abord, le calcul précédent donne une estimation de la masse des étoiles plus proches du centre
galactique que le Soleil et non pas une estimation de la masse totale de la Galaxie. D’autre part, la
Galaxie n’ayant pas une symétrie sphérique, l’application du théorème de Gauss est abusive et donne
un résultat très approximatif.
I.B.3) Ordre de grandeur de la densité d’étoiles.
( )
11
3 3
033
1 6 10
1,1 10 al
4
450 000
3
3 2
S
M
nM
D
− −
×
= = = ×
  π
π 
I.C. Généralisation de la troisième loi de Kepler
I.C.1) Expliquer pourquoi les deux étoiles ont même période.
Par définition du centre de masse, les points
1
E
, C et
2
E
sont alignés : il s’ensuit que les deux étoiles
tournent autour du centre de masse à la même vitesse angulaire.

LYCÉE DE KERICHEN MP-Physique-chimie Devoir libre n°8-2
JLH 19/03/2008 Page 2 sur 4
De plus, toujours par définition du centre de masse :
1 1 2 2
CE CE 0
m m
+ =
. Avec les définitions de
l’énoncé, cela s’écrit
1 1 2 2
m r m r
=
et donc 1
2
2 1
r
m
r m
=
I.C.2) Nouvelle expression de la troisième loi de Kepler.
Appliquons la relation fondamentale de la dynamique pour l’étoile
1
E
:
( )
2
1
1 2
2/1 21 1
2 2
1 2
d r
m m
f G e m
dt
r r
= − =
+
avec 2
1 12
1 2
m
r r
m m
=+ et
12 1 2
r r r
= +
, ce qui peut encore s’écrire :
2
12
1 2 1 2
2/1 21
2 2
12 1 2
d r
m m m m
f G e
r m m dt
= − = +
Le vecteur
12
r
, décrivant le mouvement relatif de l’étoile
2
E
autour de l’étoile
1
E
, est solution d’une
équation différentielle identique à l’équation différentielle du problème à un corps, pourvu que l’on
substitue la masse de l’étoile
2
E
par la masse réduite du système binaire
1 2
1 2
m m
m m
+.
Le même raisonnement qu’à la question I.A.2 conduit à la relation :
( ) ( )
2 2
1 2
21 2
2 2 2 2 1 2
2 2 2
1 2
1 2
4 4
m m
m m
m r m r G r r
T m m T
r r
π π
ω = = = +
+
+
Soit
(
)
3
1 2
2 2
4
G m m
d
T
+
=π ou encore
( )
3
1 2
2d T
G m m
= π +
Dans la limite où
1 2
m m
>>
, nous retrouvons l’expression de la troisième loi de Kepler du problème à
un corps démontré à la question I.A.2
I.C.3) Application numérique. La troisième loi de Kepler donne la masse totale du système binaire :
(
)
(
)
( )
3 3
2 2 12
1 2 30
1 2 2 2
11
4 4 1,5 10 1,01 10 kg 0,50
6,7 10 44,5 365 24 3600
S
r r
m m M
GT
−
π + π ×
+ = = = × =
× × × × ×
Et nous connaissons le rapport des masses par la relation 12
2 1
2
rm
r m
= =
Nous en déduisons :
( )
( )
30
1 1 2
30
2 1 2
10,34 10 kg 0,17
3
20,67 10 kg 0,33
3
S
S
m m m M
m m m M
= + = × =
= + = × =
I.D. Vitesse de libération
I.D.1) Énergie totale initiale.
La réponse attendue est assurément 2
0 0 0 0
1
2
k p
Mm
E E E mv G
R
= + = −
Mais il y a un gros problème : il est impossible de projeter directement un satellite en orbite à partir
de la surface d’une planète. La réponse ci-dessus est donc une fausse bonne réponse, aussi vrai que la
question est une fausse bonne question…

LYCÉE DE KERICHEN MP-Physique-chimie Devoir libre n°8-2
JLH 19/03/2008 Page 3 sur 4
Pas de problème par contre pour exprimer l’énergie mécanique totale d’un satellite :
2
1
2
k p
Mm
E E E mv G
r
= + = −
I.D.2) Vitesse de libération.
La vitesse de libération correspond à une énergie nulle : 2
1
0
2
lMm
E mv G R
= − =
Soit : 2
l
M
v G
R
=
I.D.3) Application numérique.
Avec
2
T
T
M
g G
R
=, la vitesse de libération terrestre a pour expression :
1
2 11,2 km s
lT T
v gR
−
= = ⋅
Il est bien entendu impensable de communiquer une telle vitesse à un projectile au sol !
Vitesse de libération solaire :
1
2 620 km s
S
lS S
M
v G R
−
= = ⋅
I.D.4) Expression de la vitesse de libération stellaire en fonction de la masse volumique de l’étoile.
3
4 2
2 2 2
3 3
S S
lS S S S
S S
M
v G G R R G
R R
ρ
= = × π = π ρ
Pour des étoiles de structure interne comparable (cela signifie-t-il de même densité ?) la vitesse de
libération est proportionnelle au rayon de l’étoile.
I.E. Étoile de Laplace
L’étoile imaginée par Laplace aurait une vitesse de libération stellaire
5 1
3 10 km s
l
v
−
= × ⋅
. Cette
vitesse était connue en 1798 comme étant la vitesse de la lumière dans le vide et Laplace en a conclu
que la lumière n’atteignant pas la vitesse de libération ne pouvait pas s’échapper d’un tel astre. C’est
ce que l’on nomme aujourd’hui un « trou noir ».
I.F. Rayon de Schwarzschild
I.F.1) Expression du rayon de Schwarzschild.
2
2
C
GM
R
c
=
I.F.2) Applications numériques. Pour le Soleil :
3,0 km
CS
R
=
. Pour la Terre :
8,9 mm
CT
R
=
.
I.F.3) Force gravitationnelle exercée par un trou noir.
2
2 2
2
C
TN
R c m
GMm
F
r r
= =
Application numérique :
33 N
TN
F
=
I.F.4) Accélération de la pesanteur.
2
18 2
5,0 10 m s
2
TN C
c
gR
−
= = × ⋅
I.F.5) « Sphère des évènements ». Aucune onde électromagnétique, aucune information, ne peut
s’échapper du trou noir. Aucun évènement se produisant à l’intérieur de cette sphère ne peut être
connu d’un observateur extérieur.

LYCÉE DE KERICHEN MP-Physique-chimie Devoir libre n°8-2
JLH 19/03/2008 Page 4 sur 4
I.G. Application au cœur de notre galaxie
I.G.1) Masse de l’objet massif présent au cœur de la galaxie.
237 7
4,4 10 kg 2,2 10
OM S
v r
M M
G
= = × = ×
I.G.2) L’objet massif en question ne saurait être une étoile : 50
OM S
M M
I.G.3) Rayon de Schwarzschild du trou noir présent au centre de la galaxie.
11
2
2 1,3 10 m 130 millions de kilomètres
OM
CGM
Rc = = × =
Le demi grand axe de l’orbite terrestre est égal à
150 millions de kilomètres
, ce qui est tout à fait du
même ordre de grandeur.
I.G.4) Cygnus X-1
Utilisons les résultats démontrés à la question I.C.3. Cette fois, c’est la masse totale du système
binaire qui est connue et l’on en déduit, par la troisième loi de Kepler, la distance relative des deux
astres :
1
3
2 10
1 2 2
9
3,0 10 m
S
M
d r r GT = + = = ×
π
On en déduit :
10 1
2
1 1
1 2
10 1
1
2 2
1 2
0,5 10 m et 66 km s
2,5 10 m et 325 km s
m
r d v
m m
m
r d v
m m
−
−
= = × = ⋅
+
= = × = ⋅
+
La vitesse de la Terre sur son orbite est égale à
1
30 km s
−
⋅
, valeur inférieure aux deux vitesses
calculées ci-dessus alors que le rayon de l’orbite a pour valeur
10
15 10 m
×, valeur bien supérieure aux
deux rayons calculés ci-dessus.