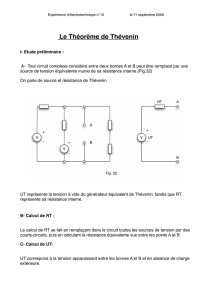
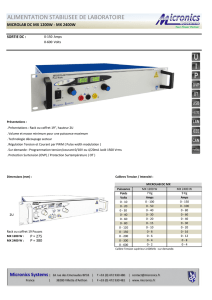
On considère le circuit :

NOM : Pr. Gérard PRIEUR
Prénom : Calculatrices autorisées Durée 2H00
Devoir surveillé du17 janvier 2012
Circuit à Amplificateur opérationnel
Soit le circuit suivant :
1) Exprimer la tension VS1 :
100
1
1
V
VS   
2) 0n applique le théorème de Thévenin entre A et B, la tension du générateur de Thévenin est :
Si Vs1 = +12 alors V1 < 0.119
Si Vs1 = -12 alors V1 > - 0.119
Si Vs1 = +12 alors V1 < - 0.119
Si Vs1 = -12 alors V1 > + 0.119
VTH = 12 volts  V
TH = 6 volts  V TH = 3 volts 
3) Et la résistance interne de Thévenin est :
RTH = 20 kΩ  R
TH = 10 kΩ  R TH = 5 kΩ 
Circuit à Diode
4) Dans quel cas la diode D1 conduit ?
Si Vs1 > 6 volts  Si Vs1 < 6 volts  Si Vs1 > 0 
5) Si D1 conduit on peut écrire :
Vs2 = 2
61Vs  Vs2 =
4
121*2
Vs  Vs2 =
3
121
Vs 
6) Quand D1 ne conduit pas, on peut écrire :
Vs2 = 2
61Vs  Vs2 = Vs1  Vs2 =
3
121
Vs 

Circuit Complet
A t = 0+ Vs1 = -12
7) Pour quelle valeur minimum de E la tension de sortie Vs1 sera rectangulaire ?
E = 0,6 volt  E = 0.238 volt  E = 0,119 volt 
8) Avec E = 1 volt, quel est le rapport cyclique η de la tension de sortie Vs1 :
η = 50%  η = 33 %  η = 25 % 
9) Avec E = 0.6 volt à quel instant t1 de la première période Vs1 passe de l’état bas à l’état haut ?
t1 = 51,9 µs  t1 = 48,9 µs  t1 = 1,90 µs 
10) Quelle est la valeur minimum Vs3m de Vs3
Vs3m = -12 volts  Vs3m = - 6 volts  Vs3m = + 6 volts 
11) Quelle est la valeur maximum Vs3M de Vs3 :
Vs3M = +12 volts  Vs3M = + 8 volts  Vs3M = + 6 volts 
Transistor FET BC264D
Soit le montage d’étude des caractéristiques du BC264D :
On relève les caractéristiques (idéalisées) suivantes :
V2 > Vp > Vp > Vp
V1 0 volt -0,5 volt < - 1,5 volts
ID 6 mA 3 mA 0 mA
On cherche alors à identifier les paramètres de l’équation :
n
GS
DSSD Vp
V
II 
 1.
12) Quelle valeur donnez-vous à IDSS ?
6 mA  3 mA  1 mA 
13) Quelle valeur donnez-vous à Vp ?
+ 1 volt  - 1,5 volts  +1,5 volts 
14) Quelle valeur donnez-vous à n ?
1,632  1,71  1,732 

15) Si on utilise ce transistor avec un courant de repos de 2 mA. Quelle est la valeur de la pente gm
de ce transistor en ce point ?
gm = 4,33 mS ± 5%
Etude dynamique de :
On admettra la compatibilité du courant de repos avec les résultats précédents.
16) Quelle est la valeur Vso de Vs au repos ?
Vso = 9,9 volts  Vso = 14,1 volts  Vso = 13,6 volts 
17) Les condensateurs étant des courts-circuits à la fréquence de travail on notera :
vs = Vs-Vso, id = Id – Ido ve = Ve-Veo
Avec les valeurs des éléments indiqués sur le schéma exprimer la valeur de l’amplification ve
vs en
fonction de la pente gm de ce transistor exprimée en Siemens :
ve
vs = - 3465 gm  ve vs = - 3300 gm  ve vs = - 3135 gm 
18 - 19) Si Ve = 3,9 + 0,5 sin ω.t exprimer, en régime permanent, (à 5% près) vs puis Vs :
vs = -16,93.ve =-8,46*sinω.t ± 5%
Vs = 14,1 - 8,46* sinω.t ± 5%
20) En considérant le réseau C2-R2 et en désirant que ce réseau n’atténue pas un signal sinusoïdal
de 20 Hz de plus de 3dB quelle valeur minimum doit avoir pour C2 ?
C2min = 7,96 nF ± 5%

Corrigé du DS du 17/01/2012
1) On a une bascule de Schmidt ou bascule à hystérésis avec entrée sur l’entrée - : la « bonne
réponse est donc : Si Vs1 = +12 alors V1 < 0.119
Si Vs1 = -12 alors V1 > - 0.119
2) VTH = 6 volts et 3) RTH = 5 kΩ
4) On a le circuit suivant (avec Thévenin) :
Vd
Id
La diode D1 conduit (Id > 0) si Vs1 > 6 volts et, 5) dans ce cas Vs2 = 3
121 Vs
6) Quand D1 ne conduit pas alors Vs2 = Vs1 (il n’y a pas de courant dans R6)
7) Nous avons une bascule à hystérésis :
dont les seuils sont + 119 mV et – 119 mV, il faut donc que E dépasse 119 mV pour avoir des
changements d’état et donc une tension rectangulaire en Vs1.
8) La tension V1 étant symétrique par rapport à l’axe des temps lorsque E dépasse 119 mV la
tension de sortie sera toujours une tension « carrée » (rapport cyclique η = 50%)
9) Ce basculement se produit lorsque V1 est décroissante et vaut – 119 mV  t1 = 51,9 µs
10) La valeur minimum Vs3m est + 6 volts (Vs1 < 6 volts)
11) La valeur maximum de Vs3 se produit lorsque D1 conduit et que Vs1 vaut +12 volts, dans ce
cas Vs3M = +8 volts
12) 13) et 14) IDSS = 6 mA ; Vp = + 1,5 volts ; n = 1,71 et  VGS = -0,5 volt
15) La pente gm =
P
GS
D
dV
dI 
=
GSP
Do
VV In
.= 789,0
10*2*71,1 3
= 4,33 mS = 4,33 * 10-3 S
16) Vso = Vcc – RD*IDo = 14,1 volts
17) gmRgm
v
vD
e
S*3300* 
18) et 19) La valeur moyenne de Ve (3,9 volts) n’est pas transmise par C2 en conséquence :
ve = 0,5 sin ω.t, on a : gm =
P
GS
D
dV
dI 
=
GSP
Do
VV In
.=
mS13,5
5.05,1
10*3*71,1 3
d’où :
vs = -gm*RD.ve = - 16,93.ve = - 8,46. sin ω.t et Vs = 14,1 - 8,46. sin ω.t
20) A 20 Hz ωo = 125,7 rad.s-1 on doit donc avoir R2.C2. ωo > 1  C2 > 7,956 nF (donc 10 nF
en pratique)