Correct - chimphys

Correction : lecture prof 5 mn, partie I : 15 mn, partie II : 8 mn
lecture élève 10 mn, partie I : 25 mn (/27 ramené à 25 soit 13/20), partie II : 15 mn (/18, 7/20 en proport°)
Partie I QUESTIONS PRELIMINAIRES :
1 ) (/3) Œil normal :
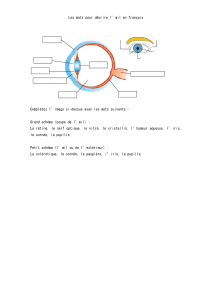
1) a) Quelle est la vergence du cristallin d’un œil normal ?
20 δ ( 0,5 )
Argumentez : D’après le Doc 4 ( 0,5 ) , C (cornée ) = 40 δ or C (oeil ) = C (cornée ) + C (cristallin)
D’où C (cristallin) = C (oeil) - C (cornée) = 60 - 40 = 20 δ
( 1 )
( 0,5 ) ( 0,5 )
Si les docs ne sont pas utilisés alors notation max (1,5)
distance OF’ = 1,5 cm soit C = 1 / OF’ = 1 / ( 1,50 × 10 – 2 ) = 66 δ
( 0,5 )
( 0,5 )
( 0,5 )
1) b) (/3) Dans le cas d’un œil normal, où se situe le punctum remotum ?
En conséquence, à quel endroit se trouve l’image d’un point objet très éloigné (situé au punctum remotum) ?
D’après le Doc 5 ( + 0,5 ) , le punctum remotum (PR) est le point le plus éloigné que l’œil puisse voir
sans accommoder ( + 0,5 ). Pour un œil normal, le PR est rejeté à l’infini ( 1,5 ) (OA (en m) = - ∞ )
Ici, le terme souligné indique que c’est une valeur algébrique (dans le sens contraire de déplacement de
la lumière, si ce dernier est choisi arbitrairement comme positif) . En conséquence, l’image d’un point
objet très éloigné (situé au PR) se trouve nette ( 0,5 ) sur la rétine ( 1 ).
2) Œil myope :
2) a) (/6) A quelle distance de l’œil se situe le punctum remotum pour l’œil myope de Monet, en … ?
Enoncé 1 : En Sept 1922, d’après le Doc 1 ( 0,5 ), la vision de l’œil myope correspond à 1 / 10 ( 1 ).
D’après le Doc 5 ( + 0,5 ) , la myopie correspondante est de - 2,50 δ ( 1 ), ce qui correspond à une
distance OA = OPR =
1 / (- 2,50) = - 0,40 m = - 40 cm
( + 0,5 )
( 1 )
( 1 )
( 1 )
Enoncé 2 : En 1912, d’après le Doc 1 ( 1 ), la myopie correspondante est de - 1,75 δ ( 1 ).
D’après le Doc 5 (+0,5), la distance correspondante est OPRemot = 1/C = 1/(-1,75) = -0,57 m = - 57 cm
( 0,5 ) ( 0,5 ) ( 1 ) ( 1 )
( 1 )
( + 0,5 )
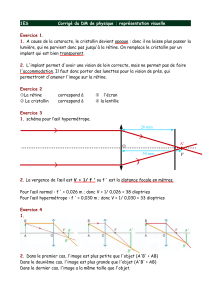
2) b) (/2) Sur le doc 5, on place le symbole de la lentille ( 0,5 ) et on trace le chemin emprunté par chacun
des 3 rayons : ils divergent après traversée lentille ( 0,5 ), puis converge ( 0,25 ) sur rétine ( 0,25 )
2) c) (/6) Quelle est la vergence de l’œil myope de Monet corrigé, en 1912 ?
L’oeil corrigé de vergence 60 δ ( 2 ) correspond à celle d’un œil normal ( 1 )
Quelle lentille de correction faut-il pour l’œil myope de Monet, en Septembre 1922 ?
Cc = - 2,50 δ ou suivant énoncé Cc = - 2,50 δ ( 2 ) + doc 1 et 4 utilisés ( 1 )
Cas Septembre 1922 L’image du PR doit être récupérée nette sur la rétine ( 1 ), OA’ = OF’œil normal
Or le PR se trouve à OP Remotum = -0,40 m ou CR = - 2,50 δ ( 1 )
La vergence de l’oeil normal (ensemble « cornée + cristallin ») est C oeil normal = 60 δ ( 1 ) , voir Doc 4 (+0,5)
On peut appliquer la loi de conjugaison :
- 1 / OPR + 1 / OF’œil myope = 1 / OF’œil normal
Ou tout simplement : C Remotum + Cœil myope = C oeil normal
( 2 )
Le calcul donne Cœil myope = - C Remotum + C oeil normal = - ( - 2,50) + 60 = 62,5 δ ( 2 )
On aurait aussi pu demander la vergence de l’œil myope :
On considère le verre correcteur de la lunette comme accolé à la cornée.
D’où C ( correction ) = C ( oeil normal ) - C ( œil myope ) = 60 - 62,5 = - 2,5 δ ( 2 )
On trouve tout simplement que le verre correcteur à utiliser correspond à la myopie exprimée en δ
3) Œil droit de Monet (ayant subit la cataracte) après opération :
3) a) (/3) Quelle est la vergence de l’œil droit, après opération, en considérant que jeune, Monet avait des
yeux normaux ? Après opération, le cristallin de l’œil droit de Monet a été enlevé ( 1 ), cet œil se
résume alors à la cornée comme unique lentille ( 1 ). En considérant que jeune, Monet avait des yeux
normaux, la vergence de l’œil droit est : Cœil opéré = C cornée oeil normal = 40 δ ( 1 )
3) b) (/4) Quelle est la vergence du verre correcteur à utiliser pour que l’œil voit nettement un objet situé à
l’infini, en considérant le verre correcteur de la lunette comme accolé à la cornée de l’œil opéré ?
Après opération, il faut récupérer la vergence d’un oeil normal ( 2 ) donc utiliser un verre correcteur
de vergence égale à celle du cristallin soit de 20 δ ( 2 ) : car C (oeil ) = C (cornée ) + C (cristallin)
Partie II : COMMENTAIRE ARGUMENTÉ : (/16) La notation par compétence est aussi enviseageable
En 20 lignes maximum, imaginez le résumé écrit du commentaire réalisé à l’oral devant Claude Monet.
Monsieur Monet,
La cataracte aux 2 yeux vous oblige maintenant à vous faire opérer, si vous voulez retrouver la vue
(même imparfaite). ( 1 )
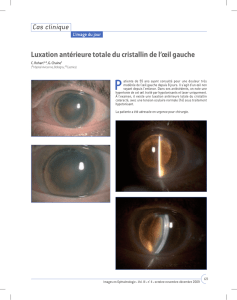
Cette maladie a engendré une opacification du cristallin ( 1 ) ( voir Doc 3 ). ( 1 )
En conséquence, vous avez remarqué une gêne visuelle due à la lumière vive ( 0,5 ) et graduellement
vous avez observé une extinction de l’image sur votre rétine ( 0,5 ), au cours de la maladie.
De plus l’image récupérée sur l’œil est devenue de plus en plus floue ( 1 ) ( voir Doc 2 ). ( 1 )
En vous opérant, on enlèvera le cristallin ( 1 ) ( voir Doc 1 ) ( 1 ). Mais votre œil n’aura plus la même
vergence ( 1 ) puisqu’il ne restera que la cornée comme lentille ( 1 ) ( voir Doc4 ) ( 1 ).
Vous devrez alors porter un verre correcteur pour l’œil droit afin de pouvoir voir de loin ( 1 )
( voir Doc 5 ) ( 1 ).
Comme votre oeil ne pourra plus accommoder ( 1 ) (rôle du cristallin), vous ne pourrez voir de près
avec cette correction ( 1 ).
De plus, vous aurez du mal à supporter la lumière (photophobie) ( 0,5 ), aurez une distorsion visuelle
des images ( 0,5 ), tout cela étant dû à l’absence du cristallin ( + 0,5 ) ( voir Doc 1 ) ( + 0,5 ) et la
technologie actuelle du verre correcteur ( + 0,5 ) .