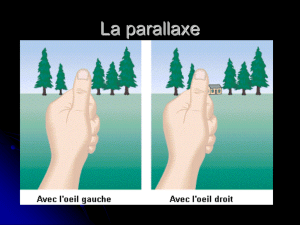
MESURER DES DISTANCES A L`AIDE DE VISEES.

1
ère
visée
2
ème
visée : six mois plus tard
Parallaxe θ mesurée
TP DE PHYSIQUE n°3 :
MESURER DES DISTANCES A L’AIDE DE VISEES.
Faire une visée consiste à aligner son œil, un repère et un point d’un objet éloigné de façon à occulter
le point éloigné par le repère.
I. MESURER UNE DISTANCE OBJET-OBSERVATEUR.
B
UT DE L ’ EXPERIENCE : Déterminer, à l’aide de visées, la distance vous séparant du tabouret posé
sur le bureau.
E
XPERIENCE : Vous reporterez toutes les mesures sur votre compte rendu.
• Tenir verticalement la règle translucide, à bout de bras.
• Viser le tabouret à travers la règle de façon à aligner la graduation 0 avec le pied du tabouret.
• Tout en restant dans la même position, lire la graduation sur laquelle s’aligne le haut du
tabouret. On la note h.
• Demander à votre binôme de mesurer la distance entre la règle et votre œil. On la note l.
• Mesurer la hauteur du tabouret posé sur le bureau. On la note H.
E
XPLOITATION :
a. Faire un schéma de la situation physique correspondant à cette expérience sans oublier les
rayons lumineux provenant des extrémités du tabouret. Faire figurer avec soin les longueurs H,
h, l et L.
b. En appliquant un théorème bien connu en géométrie, donner la relation mathématique entre H, h,
l et L.
c. Calculer L et donner sa valeur en mètre. Le résultat sera exprimé avec un nombre de chiffres
significatifs cohérent avec les mesures.
d. A l’aide d’un décamètre, mesurer L directement cette fois. Les deux valeurs trouvées pour L sont-
elles cohérentes ?
II. MESURER LA HAUTEUR DE L’OBELISQUE DE LA PLACE DE LA
CONCORDE.
A l’aide d’un double décimètre tenu verticalement à bout de bras, on vise
avec un œil l’obélisque situé place de la Concorde. La règle est placée à d
= 50 cm de l’œil et l’obélisque est occulté par une portion de règle l = 7,2
cm. L’observateur se trouve à une distance de l’obélisque égale à L = 160
m. On cherche à déterminer la hauteur H de l’obélisque.
a. Faire un schéma de la situation physique décrite (avec les rayons
lumineux provenant des extrémités du monument).
b. Donner la relation mathématique entre H, d, l et L. Justifier.
c. Calculer la hauteur H de l’obélisque. Exprimer le résultat en mètres
avec un nombre de chiffres significatifs cohérent avec les données.
d. Calculer la durée mise par la lumière pour parcourir cette distance.
Convertir cette durée en nanosecondes.
III. PARALLAXE ET DISTANCE DES ETOILES.
Les étoiles et les constellations n’occupent pas toute l’année la même position dans le ciel car la Terre
se déplace autour du Soleil au cours de l’année (voir schéma).
C’est le principe de la méthode de la parallaxe : on observe une même étoile à six mois d’intervalle (de
la Terre ou par l’intermédiaire du satellite Hipparcos) : à l’aide de ces deux visées, les astronomes sont
capables de déterminer un angle appelé parallaxe et noté θ (voir schéma). Cet angle permet de
mesurer la distance du Soleil à l’étoile considérée.
HIPPARCOS, LE GEOMETRE DES ETOILES :
C'est cette méthode qu'a employée de 1989 à 1993 le satellite
Hipparcos pour mesurer la distance des étoiles les plus proches de
la Terre. Travail colossal que celui du satellite Hipparcos : des
centaines de milliers de parallaxes ont été mesurées par ce
satellite, à raison de 115 mesures pour chaque étoile !
QUESTIONS :
1. M
ESURE DE LA DISTANCE S OLEIL – S IRIUS :
Sirius, de la constellation du Grand Chien, est l’étoile la plus brillante
du ciel nocturne. Son angle de parallaxe est de θ
1
=1,06x10
– 4
°
(donnée Hipparcos).
a. A l’aide du schéma ci-dessus, donner la relation entre tanθ
1
, le rayon R de l’orbite terrestre et la
distance D
1
entre le Soleil et Sirius.
b. Calculer numériquement la distance D
1
. Donnée : R = 150 x 10
6
km.
2. M
ESURE DE LA DISTANCE S OLEIL – ETOILE POLAIRE :
L’étoile polaire, de la constellation de la petite ours a longtemps aidé les marins qui avaient perdu le nord.
Elle est visible tous les jours dans le ciel nocturne d’Epinay sur Seine. Son angle de parallaxe est
d’environ θ
2
=1,94x10
– 6
° (donnée Hipparcos).
a. Donner la relation entre tanθ
2
, le rayon R de l’orbite terrestre et la distance D
2
entre le Soleil et
l’étoile polaire.
b. Calculer numériquement la distance D
2
. Donnée : R = 150 x 10
6
km.
c. Calculer la durée mise par la lumière pour parcourir cette distance. Convertir cette durée en
années.
IV. LES VOYAGES DE LA LUMIERE.
Compléter le tableau ci-dessous. Dans la colonne 4, convertir la durée de la colonne 3 dans l’unité
indiquée. Détailler les calculs dans le compte-rendu.
Distance en
mètres
Temps mis par la lumière
pour parcourir cette
distance (en secondes)
Temps convertit
Distance table élève du I- ns
Distance Soleil-Pluton 5,87 x 10
12
heures
Distance Terre-étoile polaire années
Diamètre de la galaxie 10
21
années