Travail8-Ch9 - Monopole - Enonce - WebCampus

Préparation des chapitres
9 et début 10
Traitez deux questions parmi les quatre (au choix)
Solutions écrites à remettre pour le lundi 16/11 à 13h au plus tard
- Dans la rubrique « Travaux » de Webcampus SECO B201 ou
-Par e‐mail au professeur : [e-mail] ou
- Dans la boite aux lettres du professeur, Bureau 532 (5e étage).
Obligatoire pour les étudiants du 1er tiers de l’ordre alphabétique
ECGE2 de K à P, MATH2 de E à M.
Groupes de 2 étudiants maximum –1 copie par étudiant mentionnant les
noms des équipiers ou collaborateurs
Nommer les fichiers: T08 Nom de l’étudiant
Questions : [e-mail]
SECO B201 –ECGE B170
ECONOMIE –Cours interactif –8eEnoncé
1

Question 1 : Monopole (sacs)
La société belge SAKA vient de créer un nouveau sac «Duval» très tendance pour le
marché belge. L'élaboration du concept a coûté 4000 €. Les coûts variables, matières
premières et facteur travail, sont estimés à 50 euros pièce. L'entreprise estime qu'elle
pourra vendre ses sacs à 100 euros par sac.
La semaine précédente, l’exercice 2 demandait de calculer :
1) Calculez la quantité seuil de profit (minimum, point mort) si la quantité est libre et si
le prix est 100€par sac. (0 point)
2) Calculez la quantité minimum que vous devez pouvoir vendre (toujours au prix de
vente de 100€par sac) pour couvrir les coûts, si vous avez déjà produit 600 sacs.
Pourquoi cette quantité est-elle différente de la sous-question (a) ? (0 points)
3) Dessinez la courbe de coût moyen et dites si vous pouvez trouver un prix seuil d’entrée
et une quantité correspondante. (0 point)
2

Question 1 : Monopole (sacs) (10 points)
a) Le directeur commercial de Zaka propose une stratégie commerciale pour la Belgique.
Il a estimé la disposition à payer des consommateurs pour le sac Duval (demande
collective inverse) à P= 550 –0,5 Q. Il se considère en monopole et considère que la
fonction de coût est correcte. Comment peut-il déterminer la quantité qui maximise
le profit et à quel prix peut-il vendre le sac ? Quel sera le profit total? (3 points)
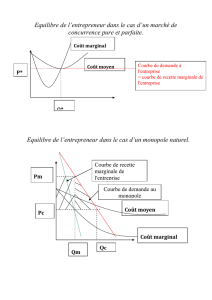
b) Dans l’espace prix/quantité, tracez la droite de demande, la droite de recette
marginale, la courbe de coût moyen (CM) et la courbe de coût marginal (Cm).
Identifiez la quantité de monopole, le prix de vente et le profit calculés à la sous-
question précédente. (2 points)
c) Distinguez la représentation traditionnelle du « surplus » du producteur et la
représentation de son profit dans l’espace P,Q (en utilisant les données des deux
sous-questions précédentes). (2 points)
d) Expliquez les différences entre le projet initial (à prix donné –énoncé de la semaine
passée, repris à la dia précédente) et l’optimisation de monopole. Si le monopole veut
vendre davantage de pulls, voudra-t-il les vendre en Belgique ou essayer de trouver
un autre marché totalement séparé du marché belge (sans possibilité de revente en
Belgique) ? Expliquez. (3 points)
3

Question 2 : Cartel (10 points)
Imaginez le marché des taxis de l’aéroport au centre-ville (2 points par sous-question)
–Demande collective : Q=200-10P
–Offre collective : Q = 10P-20
a) Représentez graphiquement l’offre et la demande et calculez la quantité et le prix à
l’équilibre concurrentiel.
b) Donnez l’expression mathématique de la fonction de recette marginale d’un
monopoleur potentiel sur ce marché. Comparez-la à l’expression de l’élasticité de
la demande au prix (fonction de Q).
c) Supposez qu’une centrale de réservation commune à tous les taxis puisse obtenir
autant de courses en taxi qu’elle veut à condition de payer P=2+(Q/10) par taxi
qu’elle met en service. Supposez, en outre, qu’elle a le monopole de l’accès aux
taxis. Quelle est la quantité et quel est le prix qu’elle choisit de pratiquer ?
d) (O point, par curiosité) Donnez l’expression mathématique de l’élasticité de la demande au
prix pour toute la courbe de demande (écrivez-la comme une fonction de Q) et calculez sa
valeur à l’équilibre concurrentiel.
Comparez l’équation de la recette marginale à l’équation de l’élasticité de la demande au prix
(fonction de Q). Calculez la valeur de l’élasticité de la demande au prix à l’équilibre de
monopole. Pourquoi est-elle supérieure à 1 ? Quel est l’incitant du monopoleur à monter le
prix plutôt qu’à augmenter la quantité ?
e) Il y a-t-il un incitant à la formation d’un cartel ou d’une centrale de réservation
unique des taxis ? [un argument graphique suffit. Si vous voulez calculer des
profits, utilisez CT(q)=(1/2)(4q+q2+81), et considérez qu’il y a 10 taxis donc Q=10q]
f) Il y a-t-il un incitant pour un taxi individuel à éviter la centrale de réservation?
Expliquez le problème qui surgit en utilisant le concept d’équilibre non-coopératif
du dilemme du prisonnier. Supposez qu’il y a 10 taxis. 4

Question 3 : Monopole (tableau)
•Le tableau reprend les différentes valeurs des différents coûts et
recettes possibles de la petite entreprise de votre meilleur ami (en
situation de monopole).
a) Complétez le coût moyen (CM), le coût marginal (Cm), la recette
marginale (Rm) et le prix unitaire (P) dans le tableau ci-dessus.
Utilisez le tableau pour prouver que l’entreprise de votre ami se
trouve bien en situation de monopole, et non en situation de
concurrence parfaite. (2 points)
5
QCT CM Cm RT
Rm
P
0 6 0
112 30
220 50
330 66
444 80
560 90