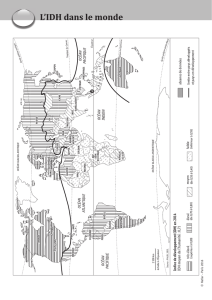
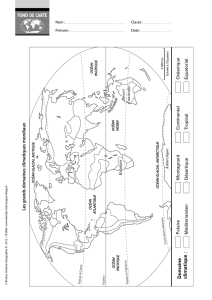
Couche limite atmosphérique
Couche limite atmosphérique
Micrométéorologie
Théorie de la longueur de mélange
Prandtl, 1925
Conditions d’applicabilité:
1) neutralité statique;
2) le profil vertical des autres quantités moyennes
doit être une fonction linéaire de z
0
z
cst
z
Théorie de la longueur de mélange
Paramétrisation du flux d ’humidité
q
qz
z
u
uz
z
0
0
uw cu u
zw c z
uz
w cu
z
Stull, fig. 6.1
Théorie de la longueur de mélange
Paramétrisation du flux d ’humidité
q
qz
z
u
w c z
z
2
() uq
E R Stull w q c z zz
2
z
Est la variance des déplacements turbulents de la
parcelle.
Théorie de la longueur de mélange
Paramétrisation du flux d ’humidité
2
z
Est la variance des déplacements turbulents de la
parcelle.
2
l c z
Longueur de mélange turbulent
Signification physique ???
2
() E
u q q
E R Stull w q l K
z z z
2
Eu
Klz
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
1
/
32
100%
