Génération de courant

Génération de courant dans les tokamaks
1. Les enjeux
2. Les courants dans un plasma de tokamak
3. Description cinétique de la génération de courant
4. Revue des différentes méthodes (théorie/expérience/technologie)
Courant auto-généré (bootstrap)
Courant inductif (Loi d’Ohm)
Courant Radio-Fréquence (LH, EC)
Courant par injection de particules (IdN)
5. Fonctionnement non-inductif du tokamak
6. Vers le réacteur continu
7. Techniques de mesure

- Les enjeux -

Les courants dans les plasmas de tokamak jouent un rôle
majeur pour
• l’équilibre magnétique de la configuration
•la stabilité MHD de la décharge
•les performances fusion (critère de Lawson, ignition)
La maîtrise des courants dans les plasmas est donc au cœur de la
physique de la fusion par confinement magnétique de type
tokamak afin d’obtenir
•un fonctionnement continu (évite les fatigues mécaniques
structurelles)
•un réacteur économiquement viable.

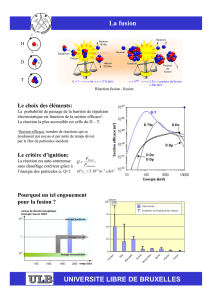
•Confinement assuré par la
combinaison de deux
champs magnétiques :
–champ axial produit par les
bobines toroïdales Bt
–champ poloïdal créé par le
courant plasma B
q
•Forme hélicoïdale des lignes
de champ évite la dérive
verticale des particules
•Equilibre MHD: jxB= p
•Rôle clé du courant plasma
Equilibre magnétique du tokamak

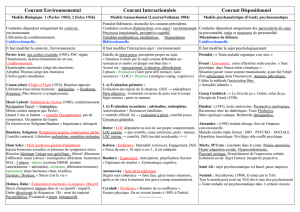
Stabilité du confinement
1.2
0.8
0.4
0.0
Ip (MA)
4
3
2
1
0
RF Power (MW)
IpPLH
PICRH
#28204
3.0
2.0
1.0
0.0 20151050 Time (s)
Te0 (keV)
q0 [sim.] M.H.D. activity
Sawtooth