Exercices Objectif BAC Les exercices suivants sont

Exercices Objectif BAC
Les exercices suivants sont des exercices de type BAC (nouveau BAC 2013) et ont pour
objectif de préparer l’épreuve écrite.
1
Intérêt de l’astronomie infrarouge pour l’étude des nuages interstellaires
Le document doit faire apparaître les notions suivantes. Les expressions surlignées doivent
obligatoirement être citées sous une forme équivalente.
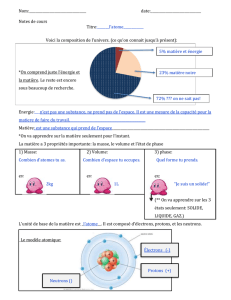
Les nuages de poussières créent des zones obscures en lumière visible à cause de la diffusion
et de l’absorption.
- Les poussières renvoient la lumière dans toutes les directions. C’est la diffusion.
- L’importance de la diffusion diminue lorsque la longueur d’onde augmente. Par suite,
les rayonnements infrarouges sont moins fortement diffusés.
Il en résulte que les nuages de poussières peuvent être transparents dans certains
domaines du rayonnement infrarouge, ce qui permet d’observer des objets cachés par
les nuages.
- L’énergie lumineuse des étoiles voisines est transformée en énergie thermique. C’est
l’absorption.
- Grâce à cette énergie thermique, les nuages émettent un rayonnement thermique. La
température d’un nuage de poussières est très basse et ce rayonnement thermique n’est
intense que dans le domaine infrarouge.
Par suite, on peut étudier la structure d’un nuage en l’observant en infrarouge.
Commentaire du document 3
Sur la photographie B, on aperçoit un grand nombre d’étoiles qui n’apparaissent pas sur la
photographie A.
On attend surtout que l’explication suivante soit proposée : le rayonnement infrarouge étant
faiblement diffusé, on voit sur la photographie B de nombreuses étoiles qui, en lumière visible
(photographie A) sont dissimulées par les nuages de poussières.
On appréciera que l’argument suivant soit en plus mentionné : des étoiles trop froides pour
émettre dans le visible peuvent apparaître dans ce domaine de rayonnement.
On remarque que, sur les photographies B, C et D, le nuage est de plus en plus brillant alors
que la longueur d’onde d’observation augmente.
Sur la photographie B, le nuage est peu visible parce que sa température est très basse et le
rayonnement thermique qu’il émet dans ce domaine est encore très faible.
Sur les photographies C et D, le rayonnement thermique devient intense dans le domaine de
rayonnement étudié. Le nuage est très brillant sur la photographie D, ce qui indique que le
nuage y est photographié dans un domaine de longueur d’onde voisin de son maximum
d’émission.
-----------------------------------------------------------------------------------------------------------------

2
Partie A. - Une onde mécanique progressive est le phénomène de propagation d’une
perturbation sans transport de matière, mais avec transport d’énergie.
- Mesure de la célérité du son dans le fil :
Première méthode
Détermination du retard τ : le retard correspond à 4 divisions, pour une sensibilité de
5 ms/div donc  = 5 × 4 = 20 ms.
Calcul de la célérité v : v =
D
τ
=
3
20
20
10
−
×= 1×10
3
m⋅s
-1
.
Deuxième méthode
Période de l'onde qui se propage dans le fil : la période correspond à 5 divisions, pour
une sensibilité de 1ms/div donc T = 1 × 5 = 5 ms.
Calcul de la célérité v de cette onde : l’onde est sinusoïdale donc,
v =
T
λ
=
3
5,0
5 10
−
×= 1×10
3
m⋅s
-1
Partie B. - Les signaux électriques correspondent à la somme de deux sinusoïdes de même
amplitude et de fréquence différente.
- Allure des spectres correspondant aux touches 2 et D :
Partie C.
1. Chaîne de transmission :

2. Le signal transmis est un signal électromagnétique. La propagation est guidée dans les
câbles de télécommunication et libre dans l’air ou le vide.
3. Contrairement aux satellites à défilement, les satellites géostationnaires sont fixes dans le
référentiel terrestre, on connaît leur position : les signaux électromagnétiques peuvent donc
être envoyés dans leur direction.
La durée minimale ne tenant compte que de l’aller-retour de l’onde électromagnétique est :
t =
4
5
2 2 3,6 10
3 10
D
c
× ×
=× = 0,24 s
-----------------------------------------------------------------------------------------------------------------
3 1. a. Les cuvettes sont situées dans le polycarbonate.
b. L’intérêt est qu’elles sont ainsi protégées des rayures et des poussières. Elles sont en effet
très peu profondes et seraient très vite abimées si elles étaient à l’extérieur.
c. Les plats et les cuvettes du CD se déplacent à vitesse constante devant le laser. On peut
donc utiliser la relation d = v∆t :
d = 1,2 × 231,4×10
−9
= 2,8×10
−7
m = 0,28 µm
d. Dans le polycarbonate, les ondes électromagnétiques se déplacent moins vite que dans le
vide. La longueur d’onde est donc plus courte :
λ =
0
n
λ
=
780
1,55
= 503 nm
2. a. Les ondes qui se réfléchissent sur le plat et les ondes qui se réfléchissent sur le fond
d’une cuvette sont cohérentes et peuvent interférer. Si l’éclairement est minimal, c’est que les
interférences sont destructives.
b. La lumière faisant un aller-retour, la différence de marche est égale à 2 e .
c. La plus petite profondeur correspond à la plus petite différence de marche qui donne des
interférences destructives.
δ =
(2
2
)
1
k
+ λ
est minimale pour k = 0
2e =
2
λ
e =
4
λ
= 126 nm = 0,126 µm
d. L’éclairement de la photodiode n’est pas nul car les deux faisceaux qui interfèrent n’ont
pas la même intensité. La partie du faisceau qui se réfléchit sur le plat est plus importante que
celle qui se réfléchit sur le fond de la cuvette.
-----------------------------------------------------------------------------------------------------------------
4

Partie A. a. Calculons l'allongement x et le rapport
x
m
pour chacun des deux ressorts :
Ressort 1
m (g) 10 20 30 40
l
eq
(cm) 3,8 4,6 5,4 6,2
x = l
eq
– l
0
(cm) 0,8 1,6 2,4 3,2
x
m
( cm⋅
⋅⋅
⋅g
-1
) 0,08 0,080 0,080 0,080
Ressort 2
m (g) 10 20 30 40
l
eq
(cm) 3,2 3,4 3,6 3,8
x = l
eq
– l
0
(cm) 0,2 0,4 0,6 0,8
x
m
(cm⋅
⋅⋅
⋅g
-1
) 0,02 0,02 0,02 0,02
On vérifie donc bien que pour chaque ressort, le rapport
x
m
est constant : l'allongement x est
proportionnel à la masse m .
b. Le coefficient de proportionnalité entre x , m ,
g
k
, a pour unité SI le m⋅kg
–1
.
Puisque g , le champ de pesanteur, s'exprime lui-même en N⋅kg
–1
, on en déduit que k (=
mg
x
)
s'exprime lui-même en N⋅m
–1
.
c. Le coefficient de proportionnalité correspondant au ressort 2 est quatre fois plus faible que
pour le ressort 1. Puisque le champ de pesanteur est constant, c'est nécessairement que la
constante de raideur du ressort 2 est quatre fois plus grande que celle du ressort 1 :
1 2
4
g g
k k
= ×
équivaut à k
2
= 4k
1
(0,08 = 4 × 0,02)
Remarque : on peut calculer les valeurs numériques des constantes de raideur, mais les
arrondis ne jouent pas en notre faveur...
k
1
=
–2
–3
9,8
0,080 10
10
× = 12 N⋅m
–1
k
2
=
–2
–3
9,8
0,02 10
10
×= 49 (5×10
1
avec un seul CS) N⋅m
–1
Partie B. 1
er
bloc de questions
a. Si on compare les graphiques des expériences 1 et 3 d'une part, 4 et 5 d'autre part (on
souhaite que seul le paramètre masse varie), on constate dans les deux cas que la période des
oscillations augmente lorsque la masse augmente. On peut préciser que lorsque la masse
quadruple, la période double :
T
3
= 2T
1
= 0,36 s et T
5
= 2T
4
= 0,18 s

b. Si on compare désormais les graphiques des expériences 1 et 4 d'une part, 3 et 5 d'autre
part, on constate que la période des oscillations diminue lorsque la constante de raideur
augmente. On peut préciser que lorsque la constante de raideur quadruple, la période est
divisée par deux :
T
4
=
1
2
T
= 0,09 s et T
5
=
3
2
T
= 0,18 s
c. Entre les deux expériences 1 et 2, seule l'élongation initiale change. Si l'amplitude des
oscillations est directement affectée par ce facteur, on constate que la période des oscillations
est strictement la même : T
1
= T
2
= 0,18 s
d. Par analyse dimensionnelle :
dim T = dim m
α
× dim k
β
(puisque c est sans dimension)
Or : dim T = T ; dim m = M et dim k =
(
)
dim force
L
= MLT
–2
L
–1
= MT
–2
On extrait de l'équation T = M
α
× (MT
–2
)
β
le système suivant :
1 = - 2 β et 0 = α + β
d'où : α = -β = +
1
2
e.
m
T c
k
= avec c constante : on retrouve bien que quadrupler la masse revient à doubler la
période, et que quadrupler la constante de raideur revient à diviser par deux la période.
Partie B. 2
e
bloc de questions.
a. Lorsque m
1
= m
2
= m, on trouve que µ =
2
2
m m
m m
=
+
: la masse réduite correspond donc à la
moitié de chacune des masses.
b. Lorsque m
1
<< m
2
, on trouve que µ =
1 2 1 2
1 2 2
m m m m
m m m
+≈
= m
1
: la masse réduite correspond
donc à la masse négligeable.
Partie C. 1. a. Par définition, σ =
1
λ
. Par ailleurs, on sait que pour une onde
électromagnétique : λ =
cT
c étant la célérité de l'onde électromagnétique (de la lumière) dans le vide : c = 3,0×10
8
m⋅s
–1
.
b. On en déduit donc que :
σ =
1
cT
c. Puisque la période de l'onde électromagnétique doit coïncider avec celle des oscillations
libres de la liaison, on en déduit que :
σ =
1
cT
=
1
2
k
c×
π µ
et donc : k = µ × 4π
2
σ
2
c
2