A-5 La genèse d`une situation fondamentale pour l

ULYSSE 1
Théorie des situations
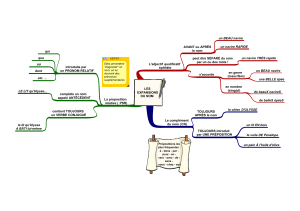
L’élaboration d’une situation
didactique pour introduire la
désignation, l’égalité et le signe
d’égalité

ULYSSE 2
•Aujourd’hui on peut considérer les mathématiques comme des systèmes de
« symboles » construits et définis formellement, sans référence « directe » à
des objets non mathématiques.
•Nous allons ici considérer que, pour les élèves au moins, la totalité des
assemblages mathématiques sont des « signifiants potentiels » dénués de
signifiés.
•Les signifiés originels de ces signifiants mathématiques seront les situations où
ils sont apparus.
•Nous étudions ces associations « situation signifiée/ texte signifiant » aussi
bien pour concevoir des situations nouvelles que pour décrire et comprendre
les situations « naturelles » observées.
•Note : On peut cependant distinguer des signifiants : par exemple un symbole
nouvellement introduit, et des signifiés, par exemple l’assemblage auquel ce
symbole peut se substituer. Une définition est donc un signe. Mais on pourrait
aussi considérer l’assemblage comme le signifiant, et le symbole comme le
signifié.

ULYSSE 3
En mathématiques, qu’exprime
l’égalité A = B
•Il existe de très nombreuses façon équivalentes de définir la
relation d’égalité.
•La plus connue s’appuie sur la théorie des ensembles: « A=B »
est synonyme de « AB et BA ». On sait que cette relation est
réflexive (A=A), symétrique (si A=B alors B=A) et transitive (si
A=B et B=C alors A=C) Mais il n’est pas facile, parfois, de la
distinguer d’une équivalence.
•Nous choisissons celle de la théorie des modèles : « A=B » si:
•a. dans toutes les occurrences de A dans des formules d’une
théorie, A peut être remplacé par B (et réciproquement) sans
changer la validité de ces formules
•b. si dans toutes les réalisation de cette théorie, A=B est la
relation d’identité: A et B sont le même objet.
•Il existe donc dans cette théorie un quantificateur !E qui exprime
qu’il existe un et un seul objet E (réalisations égalitaires)

ULYSSE 4
La désignation
•A et B sont des signifiants, leur signifié est le même et il est le seul. A et B
sont deux façons de désigner un même objet. La désignation est une
correspondance élémentaire entre un élément du modèle et l’assemblage
correspondant dans la théorie.
•Elle peut être définie par la situation suivante:
Dans une situation S, un actant X doit utiliser un objet matériel A pour
réaliser le projet défini par S mais il n’en dispose pas. Il sait qu’un autre actant
Y, distant, possède cet objet parmi plusieurs autres. Les deux agents sont
souvent dans des situations similaires, et X a besoin tantôt d’un objet tantôt
d’un autre.
•Ils doivent coopérer pour élaborer un langage simplifié dans lequel les objets
dont a besoin X seront désignés chacun par un symbole différent. A, B, C, etc.
•L’usage de ce « code » résout leur problème et A est le signifiant d’un objet
bien précis parmi les autres.

ULYSSE 5
I
G
E
C
…
A
Y
XA
Message
fourniture
X a besoin d’une pièce pour
compléter son ellipse
Suivant le code, il adresse le
message A au magasinier Y
Y choisit la pièce désignée
par A et l’envoie à X
X vérifie l’adéquation de la
pièce fournie
J
H
F
D
…
B
T
ZB
Message
fourniture
Deux autres actants Z et T
font la même chose plus
loin, mais avec un code
différent