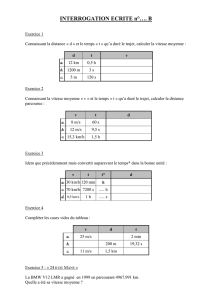
surfaces volumes

http://joho.monsite.orange.fr/
http://joho.monsite.orange.fr/
MATHS
Notion de base PDF
Formules 1 à 36 « Géométrie »
Géométrie Surface d’un triangle Surface d’un triangle équilatéral
Surface d’un triangle isocèle Surface d’un triangle scalène L’hypoténuse d’un triangle rectangle
Côté d’un triangle rectangle Surface d’un triangle rectangle Diagonale d’un carré
Surface d’un carré Diagonale d’un rectangle Surface d’un rectangle
Surface d’un losange Surface d’un parallélogramme Surface d’un trapèze
Surface d’un pentagone régulier Polygones réguliers et irréguliers Surface d’un hexagone régulier
Périmètre d’un cercle Surface d’un cercle Longueur d’un arc de cercle
Surface d’un secteur circulaire Surface d’une couronne circulaire longueur d’une hélice
Surface d’un segment de parabole Surface d’une ellipse volume d’un cube
Volume d’un parallélépipède Volume d’un cylindre Volume d’un cylindre creux
Volume d’un anneau à section carrée Volume d’un tore Surface d’une sphère
Volume d’une sphère Surface d’une calotte sphérique Volume d’une calotte sphérique
Volume d’une paraboloïde
Retour au sommaire Bas de page
Rappel PI ( 3.14159265358979 )
FORMULAIRES MATHÉMATIQUES « GÉOMÉTRIE » 1
ère
PARTIE
GÉOMÉTRIE
Il peut arriver que l’on ait besoin de connaître les dimensions, surfaces ou volumes d’objets quelconques, et
cela quand il n’est pas facile, ou même tout à fait impossible, d’effectuer des mesures directes. Il faut alors
procéder à des calculs.
Par exemple, il peut se présenter des cas où il est nécessaire de connaître la longueur d’une spire, la
section d’un conducteur, la section ou le volume d’un noyau magnétique...
En général, il s’agit de problèmes que l’on peut résoudre rapidement en appliquant une formule appropriée
de géométrie.
Nous trouverons donc dans cette leçon d’aide mémoire les formules de géométrie ayant une application
pratique en électronique.
FORMULE 1 - Calcul de la surface d’un triangle connaissant les valeurs de la base et de la hauteur (figure
1-a).

http://joho.monsite.orange.fr/
http://joho.monsite.orange.fr/
FORMULE 2 - Calcul de la surface d’un triangle équilatéral, « triangle ayant trois côtés égaux » (figure 1-b)
connaissant la longueur du côté.
Exemple (figure 1-b) :
Donnée : c = 5 cm
Surface : S 0,433 x 5
2
= 0,433 x 25 = 10,825 cm
2
FORMULE 3 - Calcul de la surface d’un triangle isocèle « triangle ayant deux côtés égaux » connaissant la
valeur des côtés égaux et de la base.

http://joho.monsite.orange.fr/
http://joho.monsite.orange.fr/
FORMULE 4 - Calcul de la surface d’un triangle scalène « triangle ayant trois côtés inégaux » connaissant
la longueur des côtés.
Dans cette formule «p» désigne le demi-périmètre, c’est-à-dire la demi-somme des trois côtés. Avant
d’appliquer la formule, il faut calculer à part la valeur «p» du demi-périmètre.
FORMULE 5 - Calcul de l’hypoténuse d’un triangle rectangle connaissant les deux autres côtés (le triangle
rectangle est un triangle ayant un angle de 90° ; l’hypoténuse est le plus grand côté, les deux autres côtés
forment l’angle de 90°). (Voir la figure 1-e ci-dessus).
FORMULE 6 - Calcul d’un côté d’un triangle rectangle connaissant les longueurs de l’hypoténuse et de
l’autre côté (pour la signification des termes, reportez-vous à la formule 5).

http://joho.monsite.orange.fr/
http://joho.monsite.orange.fr/
FORMULE 7 - Calcul de la surface d’un triangle rectangle connaissant les deux côtés de l’angle droit.
FORMULE 8 - Calcul de la diagonale d’un carré connaissant la longueur du côté. (Figure 2-a).
FORMULE 9 - Calcul de la surface d’un carré connaissant la longueur du côté.
Exemple (figure 2-a) :
Donnée : c = 50 mm

http://joho.monsite.orange.fr/
http://joho.monsite.orange.fr/
Surface : S = 50
2
= 2 500 mm
2
FORMULE 10 - Calcul de la surface d’un carré connaissant la longueur de la diagonale.
S = d
2
/ 2
S = surface
d = diagonale
Exemple (figure 2-a) :
Donnée : d 70,70 mm (valeur approchée établie avec la formule 8)
Surface : S 70,70
2
/ 2 = 4 998,49 / 2 = 2 499,245 mm
2
Comparez ce résultat avec celui obtenu en appliquant la formule 9. La différence de 0,755 mm
2
(2 500 - 2
499,245 = 0,755) est due à l’introduction de la valeur approchée de 70,70 dans le calcul de la surface, mais
l’erreur qui en résulte est très faible (seulement de 0,03 %), donc pratiquement négligeable.
(Pour faciliter la lecture, nous reportons la même figure ci-dessous à savoir figure 2).
FORMULE 11 - Calcul de la diagonale d’un rectangle connaissant les valeurs de la base et de la hauteur.
(Cette formule ci-dessus est similaire à la formule 5).