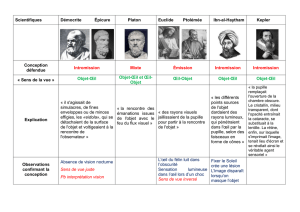
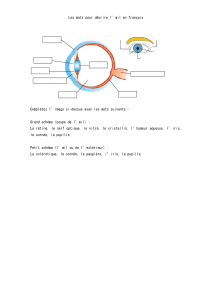
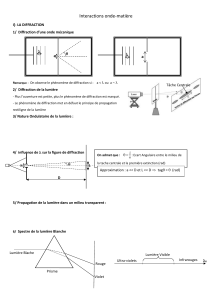
Nom du cours : Nom du cours : Fascicule 1 : Optique de Fourier

Nom du cours : Optique cohérente Nom du cours : Optique cohérente
Fascicule 1 : Optique de Fourier Fascicule 1 : Optique de Fourier
Cursus/option : M2 « Optique et Photonique »
Date de mise à jour : octobre 2006
Année scolaire : 2007/2008 Auteur : Pierre Chavel

1
INTRODUCTION :
Ceci est le premier fascicule du cours d’Optique cohérente. Il s’intitule « Optique de Fourier » et comporte
quatre chapitres et un appendice. Seuls les trois premiers chapitres donnent lieu à examen.
Chapitre I : filtres linéaires homogènes
Chapitre II : filtrage des fréquences spatiales en éclairage cohérent (vu en TD)
Chapitre III : filtrage des fréquences spatiales en éclairage spatialement incohérent
Compléments :
Chapitre IV : échantillonnage et degrés de liberté
Appendice sur la diffraction de Fresnel et la diffraction de Fraunhofer
Bibliographie recommandée :
• P.M. Duffieux, l’intégrale de Fourier et son application à l’Optique, édition originale chez l’auteur, Besançon, 1946 ;
réédition Masson, vers 1980.
• A. Maréchal et M. Françon, Diffraction, structure des images, Ed. Revue d'Optique, Paris, 1ère édition 1959, réédité
chez Masson vers 1975.
• S. Lowenthal et Y. Belvaux, « progrès récents en optique cohérente, filtrage des fréquences spatiales, holographie »,
Revue d’Optique, 46 (1967) 1-64.
• J.W. Goodman, Introduction to Fourier Optics, McGraw Hill, 2ème édition fortement remaniée, 1995 ; troisième édition
chez Roberts Publishers, 2004 ; il existe une version française de la 1ère édition traduite par J. Perez chez Masson vers
1978.
Chap I. Filtres linéaires homogènes.
La transformation de Fourier introduit en optique la notion de fréquence spatiale : tout objet décrit par
une fonction de x et de y dont le comportement est physiquement raisonnable admet une transformée de Fourier
qui représente son contenu en fréquences spatiales. Un des principaux intérêts de cette notion est son apport à la
compréhension de la formation des images : en effet, on peut fréquemment utiliser un modèle d'instrument
d'optique dans lequel ce dernier se comporte comme un filtre linéaire homogène ; dans ce chapitre, nous
introduisons la notion de filtre linéaire homogène, très fréquente dans de nombreux domaines de la physique
fondamentale et appliquée et notamment en électronique. Son intérêt majeur est sa relation avec celle de
fréquence (spatiale ou autre).
I - DEFINITIONS ET PROPRIETES PRINCIPALES :
1.1 - Définitions :
On considère une famille de fonctions f définie dans et à valeurs dans un ensemble E. muni d'une
addition et d'une multiplication internes. (En pratique, n = 1, 2 ou 3 et E s'identifie à ).
n
R
f
2
, ou CRR
ℜnE
x= (x , x , ..., x )
1 2 n f( )
x
Une application F de la famille {f} dans elle-même est appelée filtre linéaire homogène (ou filtre linéaire
invariant par translation) si elle possède les deux propriétés suivantes :
F(f)
{f} {f}
f
1° linéarité : F est dite linéaire si pour tout , et pour tout
() ()
2
12
,E λλ ∈
{
2
12
,
}
f
ff∈, on a :
()()
(
)
11 2 2 1 1 2 2
Ff f Ff Ff λλ λ λ += + (1)
2° homogénéité (ou invariance par translation) : soit . Pour toute fonction f de {f}, soit xn
o∈Rxo
f
la fonction
définie pour tout par :
xn ∈R
() ( )
xxxx
oo
ff=− ;
Filtres linéaires homogènes

2
F est dite homogène si pour tout xo et pour tout f on a :
()
()
x
o
Ff g Ff g=⇒ =
x
o
. (2)
Exemples :
- circuit électrique R, L, C : E = , n = 1, x est le temps, f = tension appliquée au circuit, F(f) = tension entre
deux points donnés du circuit.
C
- En optique : formation d'image : E = ou
+
RC, n = 2, x, y = coordonnées objet ou image, f = l'objet, F(f) =
l'image.
1.2 - Fonction de filtrage :
Démontrons que les exponentielles sont fonctions propres de tout filtre linéaire.
(
exp 2 Ωxi π i
)
Pour tout Ω, soit la fonction f de {f} définie par :
n
∈R
() ( )
xexp2Ωxfi π =i pour tout xn
∈
R.
Posons en outre g = F (f).
()
(
)
(
)
(
)
x
x , x , x exp 2 Ωxx exp2Ωxx
o
nn
oo
fi i ππ ∀∈ ∀∈ = − =
⎡⎤
⎣⎦
ii RR o f
donc
()
o
xexp 2 Ωxo
f
if π =i
or d'après l'homogénéité
(
)
xx
oo
Ff g=
et d'après la linéarité
()
()
(
)
xexp 2 Ωx exp 2 Ωx
ooo
Ff F i f i g ππ =− =−
⎡⎤
⎣⎦
ii
donc
()
(
)
(
)
x,x,xxexp2Ωxx
nn
oo
gi π ∀∈ ∀∈ − = − iRR o g,
et en particulier pour
(
)
(
)
(
)
n
o
xx,x ,0exp2Ωxxgi π =∀∈ = −ig
g
,
donc. (3)
() ( ) ()
xexp2Ωx0gi π =i
Les fonctions
(
)
exp 2 Ωxo i π i sont donc fonctions propres de tout filtre F linéaire homogène. La valeur
propre associée, g(0), dépend évidemment de Ω et du filtre F lui-même. Elle sera notée G(Ω) et appelée gain ou
encore fonction de filtrage. (En optique, on utilise encore d'autres noms, que nous introduirons plus tard). On
voit bien sûr que la fonction gain décrit la façon dont une sinusoïde traverse le filtre linéaire homogène, la phase
du gain décrivant le déphasage de la sinusoïde.
1.3 - Réponse percussionnelle :
Considérons à l'entrée du filtre une fonction f de {f} admettant une TF :
() ( ) ( )
xΩexp 2 ΩxΩ
n
f
fi π =∫i
R
d
Ω
.
Utilisons la linéarité et la définition du gain pour exprimer la sortie du filtre :
() () ( ) ( )
() ( )
()() ( )
xx Ωexp 2 ΩxΩ
Ωexp 2 ΩxΩ
ΩΩexp 2 ΩxΩ
n
n
n
gFf Ff i d
fF i d
fG i d
π
π
π
⎡⎤
==
⎡⎤
⎢⎥
⎣⎦
⎣⎦
=⎡⎤
⎣⎦
=
∫
∫
∫
i
i
i
R
R
R
g admet donc une TF, qui est
() ()()
ΩΩgGf=
 (4)
c'est à dire que le filtre a pour effet de multiplier la TF du signal d'entrée par la fonction de filtrage. Dans (4)
apparaît un produit : calculons la TF-1 des deux membres et utilisons le théorème sur la TF des produits : avec
() ( ) ( )
xΩexp 2 ΩxΩ
n
PG i π =∫i
R
d (5)
(4) devient :
Filtres linéaires homogènes

3
() () () ( ) ( )
11
xxx xxx
n
gfP fP d=∗= −
∫
R
1
x (6)
P, dont la TF est G, est appelée réponse percussionnelle (ou parfois, mais avec un risque d'ambiguité, "réponse
impulsionnelle") du filtre F : c'est d'après (6) la réponse du filtre à une entrée constituée d'un pic de Dirac δ(x).
II - ILLUSTRATIONS :
2.1 - Un exemple en électricité :
V(t)
V (t)
R
C
1
Problème : V(t) étant quelconque, trouver V1(t).
On constate facilement que la relation entre V1(t) et V(t) est un filtrage linéaire homogène. Cherchons sa
fonction de filtrage : si
(
)(
exp 2Vt i t
)
π
ν =, alors
() ()
1
1exp 2
12
Vt i t
iRC
π
ν
πν
=+,
et donc pour V(t) quelconque (mais admettant une TF) :
()
(
)()
1exp 2
12
V
Vt i td
iRC
ν
π
νν
πν
=+
∫
R
.
La relation précédente peut de façon équivalente être exprimée comme une convolution : il faut pour cela
calculer la réponse percussionnelle :
() ()
111
Hea exp
12
t
Pt TF t
iRC RC RC
πν
−
−
⎛⎞ ⎛
==
⎜⎟ ⎜
+
⎝⎠ ⎝
⎞
⎟
⎠
,
où Hea(t) est la fonction d'Heaviside. Donc
() () ()
1Hea exp t
Vt Vt t
R
C
−
⎛⎞
=∗ ⎜⎟
⎝⎠
.
De même, à une constante dimensionnée près, l'impédance complexe d'un circuit électrique quelconque est la
fonction de filtrage qui permet de passer de la tension à ses bornes à l'intensité qui le traverse.
2.2 - Présentation empirique de la notion de réponse percussionnelle en optique :
Filtres linéaires homogènes

4
système optique
r r’
plan objet plan image
z
Considérons un point lumineux M situé dans le plan objet d'un instrument d'optique. Nous supposons
ici pour simplifier le grandissement est 1 entre un objet et son image de Gauss : les coordonnées x,y de M sont
les composantes du vecteur bidimensionnel r.
En raison des aberrations, de la diffraction, d'un éventuel défaut de mise au point, l'image d'un point
n'est pas un point mais une tache située au voisinage du point r du plan image. Désignons par O(r) l'objet. Un
objet deux fois plus lumineux donne une image deux fois plus lumineuse, et si deux objets sont présents
simultanément, l'image est la somme des images de chacun des points : il y a donc linéarité, dans des conditions
dont nous expliquerons plus loin les limites, car tel est précisément l'objet central du cours d'optique de Fourier.
Par ailleurs, si on déplace le point M de r à r1, sa tache image se déplace également de r à r1. En
première approximation, dans de nombreux instruments, la tache image ne se déforme pas beaucoup en se
déplaçant : il y a homogénéité dans le champ. Désignons par P(r') la tache image correspondant à un point
lumineux unitaire situé au centre (r=0). La tache image du point r est dans ces conditions P(r' - r).
La linéarité et l'homogénéité impliquent que l'instrument est un filtre linéaire homogène ; sa réponse
percussionnelle est P(r) et l'image s'exprime sous la forme :
I
PO=∗ (7)
c'est à dire encore
() () ( )
2
rrrrr
I
OP d
′′
=−
∫
R
.
Cependant, la présentation qui vient d'être faite est entachée d'un manque de rigueur considérable : le
mot "lumineux", les quantités physiques I et O n'ont pas été définis. Il se trouve que ces quantités physiques
dépendent de l'état de cohérence :
• en éclairage cohérent, O(r) désigne l'amplitude lumineuse complexe au niveau de l'objet, P(r) l'amplitude de
la tache image due à un objet d'amplitude δ(r), I(r) l'amplitude image. Les amplitudes dues aux différents
points s'ajoutent, il y a interférences entre elles et la relation (7) décrit la figure d'interférences des
amplitudes provenant des différents points de l'objet. L'étude de la diffraction montre d'ailleurs que la
relation (7) n'est vérifiée qu'en prenant en compte différents termes de phase qui se présentent dans
l'expérience de double diffraction (voir cours de prérequis). Le chapitre II de cette partie sera consacré à
l'examen détaillé de ce cas.
• En éclairage incohérent, O(r) désigne la luminance de l'objet, P(r) l'éclairement de la tache image due à un
objet de luminance δ(r), I(r) l'éclairement de l'image : les éclairements dûs aux différents points de l'objet
s'ajoutent, il n'y a pas d'interférences, la relation (7) décrit simplement la superposition incohérente des
différents points de l'objet. Le chapitre III sera consacré à l'examen détaillé de ce cas.
• En éclairage partiellement cohérent par contre, il n'y a pas linéarité, la relation (7) est fausse. Dans le
présent cours, ce cas ne sera qu'évoqué (voir chapitre III).
Filtres linéaires homogènes