Position relative de deux courbes 1. Principe On considère deux

Position relative de deux courbes
1. Principe
On considère deux fonction f et g définies sur leurs ensembles de définitions. Soient
f
 et
g
leurs courbes représentatives respectives. On suppose que ces courbes ont des points d’intersection.
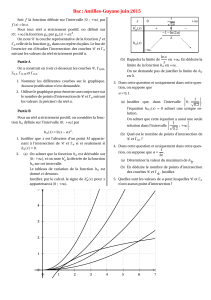
Par exemple :
Soit 0
x
l'abscisse du point d'intersection.
Graphiquement, on voit que :
- pour 0
x
x, il y a intersection.
- pour 0
x
x, la courbe de f est en dessous de celle de g
- pour 0
x
x, la courbe de f est au dessus de celle de g
On peut dire également que :
- pour 0
x
x, () ()
f
xgx
- pour 0
x
x, () ()
f
xgx
- pour 0
x
x, () ()
f
xgx
En fait, on doit "prévoir" par le calcul ce positionnement relatif des deux courbes.
Ceci revient donc à comparer les expressions ()et ()
f
xgx
Or e, mathématiques, on utilise le principe suivant :
" pour comparer deux nombres, on étudie le signe de leur différence"
Par conséquent, pour étudier la position relative de deux courbes
f
 et
g
, on étudie le signe de la
différence () ()
f
xgx.
- Dans le cas où () () 0fx gx, on en déduit que () ()
f
xgx et par conséquent
f
est au dessus de
g
- Dans le cas où () () 0fx gx, on en déduit que () ()
f
xgx et par conséquent
f
 au dessous de
g
- Dans le cas où () () 0fx gx, il y a intersection
() ()
f
xgx
x
f
0
x

2. Exemple
On considère la fonction f définie par 2 () 4 3fx x x   sur  et
f
sa courbe représentative dans un
repère (,O. Soit g la fonction définie sur  par () 2 6gx x
 et
g
sa courbe représentative dans le
repère (,O
Etudier la position relative des courbes
f
et
g
.
………….
pour étudier la position relative de deux courbes
f
 et
g
, on étudie le signe de la différence
() ()
f
xgx.
Pour tout réel x, 22
() () 2 4 6 2 10 2 6 4fx gx x x x x x
On doit donc étudier le signe de ce trinôme
…..Ce trinôme admet pour racines 11x
et 22x
D’où le tableau de signes et de conséquences :
x   1 2 + 
Signe de la différence
() ()
f
xgx
 0 + 0 
Conséquences
f
 en dessous de
g
f
 au dessus de
g
f
 en dessous de
g
Intersection intersection