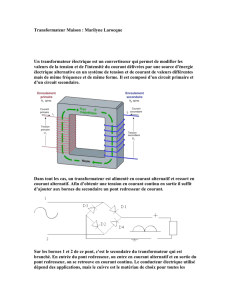
Transformateurs

Transformateurs page 1/3
TRANSFORMATEUR
VRAI FAUX
Un transformateur peut fonctionner en régime constant.
Un transformateur ne peut fonctionner qu’en régime sinusoïdale.
Un transformateur est un convertisseur de puissance électrique.
Les bornes homologues sont définies par le sens du courant.
Dans un transformateur, le rapport des tensions et le rapport des intensités s’obtiennent à
partir du théorème d’Ampère.
Le noyau ferromagnétique sert à canaliser les lignes de champ magnétique.
Dans le modèle du transformateur parfait, le rapport des tensions est toujours positif.
Dans le modèle du transformateur parfait, le rapport des intensités est toujours négatif.
Le modèle du transformateur parfait est sans perte.
Dans le modèle du transformateur parfait, si la charge est une bobine idéale, l’impédance
ramenée au primaire est équivalente à un condensateur.
Les pertes fer entraînent une élévation de température du noyau au cours du temps.
Les pertes cuivre sont inévitables dans un transformateur réel.
Les pertes par hystérésis sont réduites en utilisant un milieu dur.
Le rendement d’un transformateur réel est de l’ordre de 30%.
On réduit les pertes dans le transport de l’énergie électrique en abaissant la tension des
lignes de transport.
I-On veut réaliser un transformateur monophasé 5000/200 volts, 50 Hz et on désire que la
section du circuit magnétique soit de 1
dm
2
.
D’autre part, le champ magnétique maximal dans le noyau ferromagnétique ne doit pas
dépasser 1,5 tesla.
1) Quels doivent être les nombres de spires au primaire et au secondaire?
2) Que deviendrait ce résultat si la fréquence d’utilisation était de 60 Hz au lieu de
50?
II-On désire faire fonctionner sous une tension efficace de 220 V un récepteur absorbant une
intensité efficace 50 A avec un facteur de puissance de 0,6 arrière (inductif). Ce récepteur est situé à
l’extrémité d’une ligne bifilaire de 40 km de longueur dont chaque conducteur , en cuivre de
résistivité 1,6 × 10–8 Ω .m, a une section de 1 cm2 .
1) Quelle est la tension appliquée à l’entrée des lignes.
2) On utilise deux transformateurs parfaits identiques T
1 et
T
2;
T
1 est utilisé en élévateur de
tension et T
2 en abaisseur. Le rapport des nombres de spires est de 25. Sous quel tension faut-il
alimenter le transformateur T
1 ?
III-On considère le schéma de la figure 1.
1°) On veut se ramener au schéma de la figure 2. Déterminer l’impédance Z
r2.
2°) On réalise le montage ci-dessous et on relève les 3 courbes à droite.
I
2cc
I
1cc
y = 0,5x + 0,015
I
2cc
U
1cc
y = 29,6x + 0,5
I
2cc
2
P
1cc
y = 14x
A
2
V
1
W
A
1
R
1
L
f1
R
2
L
f2
u
1
i
1
u
2
i
2
m Z
r2
u
1
i
1
u
2
i
2
m
figure 1
figure 2

Transformateurs page 2/3
Les ampèremètres A
1
et A
2
mesurent les courants efficaces de court-circuit au primaire ( I
1CC)
et au secondaire ( I
2CC). Le voltmètre mesure la tension efficace au primaire et le wattmètre la
puissance moyenne consommée par le transformateur en court-circuit.
a) Déterminer m . Retrouver la partie réelle de Z
r2. Puis sa partie imaginaire.
b) L’essai en court-circuit peut-il servir à caractériser des pertes du transformateur en
fonctionnement nominal ?
3°) En fonctionnement nominal sur charge résistive, on constate que le rapport des valeurs
efficaces
U
U
2
1
décroît lorsque I
2
croît. Expliquer.
IV-La résistance totale des bobinages ramenée au primaire du
transformateur représenté ci-contre est R = 8 Ω . On néglige tout autre écart à
l’idéalité du transformateur.
1) Le transformateur est alimenté sous une tension sinusoïdale de
valeur efficace U
1 = 220V. La tension efficace au secondaire
à vide est de
26V.
a) Représenter le schéma équivalent du transformateur vu entre les tensions u
1 et
u
2
en utilisant la résistance R et le modèle du transformateur parfait. Déterminer la valeur numérique
de m
b) Lorsque le primaire du transformateur est alimenté et son secondaire relié à une
charge résistive R
C, la tension efficace au secondaire vaut alors
U
2 = 24V. Établir une relation entre
u
1(
t ), i
1(
t ) et u
2(
t ). En déduire les intensités efficaces I
1 et
I
2 dans le primaire et dans le secondaire.
c) Calculer la puissance moyenne fournie dans ce cas par la source au primaire du
transformateur. Calculer le rendement correspondant à ce fonctionnement.
2) Ce transformateur est utilisé en élévateur de tension: son secondaire est alimenté sous une
tension de 24V. On garde cependant les dénominations « primaire » et « secondaire » de la question
précédente pour désigner les bobinages du transformateur. C’est donc le secondaire qui est
maintenant alimenté et le primaire qui est éventuellement chargé.
a) Quelle est la valeur efficace de la tension à vide au primaire ?
b) On relie le primaire au dipôle résistif R
C. Quelle est la valeur efficace de la tension
au primaire ?
c) Calculer le rendement correspondant à ce fonctionnement et comparer avec la
valeur trouvée la question IV-1
d) Ce résultat est-il généralisable à deux transformateurs de même résistance totale
des bobinages, l’un élévateur et l’autre abaisseur de tension ?
V-Le principe d’un capteur de courant basé une sonde à effet Hall est présenté sur la figure
1. Le courant à mesurer, d’intensité I ,
circule dans un bobinage de N
1 spires (
N
1
pouvant se réduire à l’unité) placé sur un
circuit magnétique de forme torique (section
S
T, rayon moyen
r
T, périmètre moyen
ℓ
T)
muni d’un entrefer d’épaisseur e dans lequel
on glisse une cellule de Hall d’épaisseur b .
La tension
V
t R
I
b
B t
H H
( ) || ( )|
|
=
0
est
amplifiée grâce à un amplificateur
différentiel de gain A
H.. On accorde la sortie de l’amplificateur à un enroulement secondaire de
N
2
spires comme le montre la figure ( L
2 et
R
2 modélisent l’inductance de fuite et la résistance du
bobinage secondaire, R
M la résistance de mesure).
R
M
} N
1
}
N
2
V
H
I
M
V
M
e
L
2
R
2
V
S
A
H
Figure 1
i
2
u
1
u
2
m
i
1

Transformateurs page 3/3
2) On note B
M,
H
M (resp.
H
E,
B
E) les amplitudes des champs et excitations magnétiques dans
le matériau magnétique (resp.
dans l’entrefer).
a) Justifier que
B
M =
B
E =
B et trouver
l’expression de B en fonction de
µ
0,
e , I , I
M,
N
1, 2,
ℓ
T et
µ
r
(perméabilité relative du
matériau ferromagnétique constituant le tore). Simplifier cette expression dans le cas où µ
r est très
élevée (ce que l’on supposera dans la suite).
b) Déterminer la f.e.m. e
2 d’induction mutuelle aux bornes de l’enroulement
secondaire. Écrire la loi des mailles dans le circuit secondaire et en déduire une relation entre les
fonctions V
S(
t ), I ( t ) et I
M(
t ).
3) La figure 2 propose le schéma fonctionnel de ce capteur ( ϕ
C est le flux commun dans le
noyau).
a) A partir des résultats précédemment obtenus, exprimer les fonctions de transfert
H
n pour
n référencé de 1 à 7.
b) Réduire le schéma afin de mettre en évidence une chaîne directe et une chaîne de
retour sachant que I est la grandeur d’entrée et I
M la grandeur de sortie.
c) Vers quelle expression tend la fonction de transfert harmonique en boucle fermée
H j
I
I
( )ω =
M
en hautes fréquences ? A quelle condition cette valeur est-elle peu différente de
N
N
1
2
?
Que peut-on alors dire du flux commun ϕ
C
?
e) Que vaut le rapport
I
I
M
en régime continu ? Conclure sur le principe de
fonctionnement de ce capteur (rôle du noyau ferromagnétique, rôle du bobinage secondaire, rôle de
la liaison amplificateur-secondaire,....)
H
2
–
+
–
+
H
5
H
4
H
6
H
7
H
3
H
1
I
I
M
V
S
V
H
ϕ
C