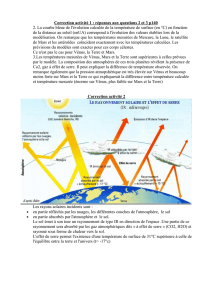
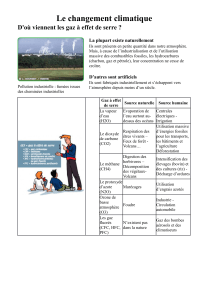
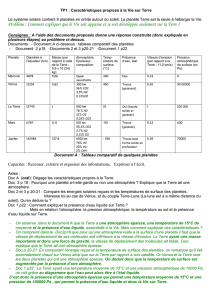
Origine, dynamique et température de l`atmosphère

Origine, dynamique et température de l'atmosphère
I) Origine de l'atmosphère de la Terre et de Mars
I-1) Datation de l'atmosphère terrestre à l'aide de l'argon
L'argon 36 est un isotope stable ne pouvant etre issu d'une désintégration radioactive. L'argon 40 n'existait pas en
quantité significative au début du système solaire. Il est produit par la désintégration du potassium 40.
a) Si l'atmosphère s'était formée récemment par dégazagee du manteau supérieur, que pourrait on dire du rapport
isotopique dans le manteau supérieur et dans l'atmosphère ?
b) On mesure le rapport dans un basalte vitrifié issu d'une dorsale océanique. Pour ce faire on chauffe la roche par
palier à différentes température. A chaque palier on mesure le rapport du gaz qui s'échappe. Les résultats sont
présentés sur a figure I-1. Dans l'atmosphère le rapport vaut 300. Que peut-on en conclure sur la formation de
l'atmosphère terrestre ?
Fig I-1: Rapport isotopique 40Ar/36Ar dans un
basalte issu d'une dorsale océanique
I-2) Datation à l'aide du xenon 129
On cherche à dater plus précisément la formation de l'atmosphère terrestre. Pour ce faire on utilise les isotopes du
xenon. En effet, le xenon 130 et 132 sont des isotopes stables dont la quantité sur Terre n'a pas varié au cours du temps
(il ne peut etre issu d'une désintégration radioactive). A l'inverse le xenon 129 n'existait pas au début du système solaire.
Il est produit uniquement par la désintégration de l'iode 129. Ce dernier a une période de demi-vie de 17 millions
d'années.
a) A l'aide du résultat présenté sur la figure I-2, estimez l'age de la formation de l'atmosphère.

Fig I-2: Rapport dans une roche basaltique issue du manteau
supérieur, divisé par ce meme rapport dans l'atmosphère.
I-3) Comparaison des rapports isotopiques de l'argon et du xénon sur
Mars et sur la Terre
Le tableau I-3 présente différent rapports isotopiques mesurés dans l'atmosphère terrestre et marsienne.
a) Comparez le rapport pour la Terre et Mars. Que peut-on en déduire sur la formation de l'atmosphère de Mars?
b) Que peut-on dire du rapport sur Mars ? Quel scénario peut-on proposer concernant la formation de
l'atmosphère de Mars expliquant à la fois les rapports et ?
fig I-3: Rapports isotopiques mesurés dans l'atmosphère de Mars et de la Terre
I-4) Vitesse de libération d'une particule dans les atmosphère de la
Terre, Mars et Vénus
La vitesse de libération d'une particule est la vitesse minimale qu'elle doit acquérir pour s'échapper de l'atmosphère
d'une planète. Pour la calculer, on suppose que la particule à l'instant initial t1 est à la surface de la Terre, animée d'une
vitesse vl. Ayant réussi à s'échapper de l'atmosphère à l'instant t2 son énergie cinétique et potentiel sont nuls.
a) En écrivant la conservation de l'énergie entre les instants t1 et t2, établir l'expression de la vitesse de libération.
b) Calculer la vitesse de libération pour la Terre, Mars et Vénus. On donne :
Terre : Mt=5.9*10^24 Kg, Rt =6370Km
Mars : Mm=641*10^21 Kg, Rm=3400 Km
Vénus: Mv=4.8*10^24 Kg, Rv=6000 Km

G=6,67 10-11 SI
c) L'énergie cinétique moyenne des molécules d'un gaz est reliée à la température par la relation
le symbole <> indiquant une moyenne : l'énergie cinétique moyenne des molécules constituant un gaz est
proportionnelle à la température.
En déduire la vitesse quadratique moyenne des molécules de dioxygène, de diazote et de l'hydrogène. On donne:
constante de boltzmann k_b = 1,38 10-23 J K-1
constante d'Arvogadro A=6,02 1023
masse molaire de l'oxygène : 16g
masse molaire de l'azote : 14g
masse molaire de l'hydrogène :1g
d) Mars peut-elle conserver son atmosphère ?
e) En réalité, toutes les molécules n'ont pas la meme vitesse dans un gaz. La distribution des vitesses suit la loi de
Maxwell Boltzmann. On donne sur la figure I-4 la distribution des vitesses des molécules d'02, H et D à une
témpérature de 300 K. Comment peut-on expliquer la différence du rapport D/H dans l'atmosphère de Mars et de la
Terre ?
Fig I-4: Distribution des vitesses des molécule d'O2, H, et D dans une atmosphère à 300 K
II) Dynamique de l'atmosphère de la Terre et de Vénus
La Terre et vénus sont des planètes de taille, masse et composition chimique proche. Toutefois, vénus tourne sur elle
meme en 243 jours terrestre. Le but de cet exercice est de voir comment cette différence affecte la dynamique globale
de son atmosphère.
a) A l'aide de la figure II-1, donner l'odre de grandeur des force de pression s'exerçant dans l'atmosphère à la surface de
la Terre. On rappelle que 1 bar =10^5 Pascal.
Figure II-1: Carte de pression à la surface de l'atmosphère en juillet

b) La force de coriolis s'exerçant sur une particule à l'équateur se déplaçant à une vitesse V vers le nord s'écrit:
fc=2*V*vitesse rotation planète (rad/s)
Calculer la force de coriolis s'exerçant sur une masse d'air à l'équateur se déplaçant à 10 km/h vers le nord sur Terre.
c) Refaire le meme calcul pour Vénus
d) L'équilibre géostrophique est-il atteint sur Vénus (on supposera que les force de pression sont du meme ordre de
grandeur que sur Terre) ?
e) En déduire combien est-ce qu'il y'a de cellules de convection entre le pole et l'équateur sur Vénus.
f) Question bonus : Vénus peut-elle avoir un champ magnétique ?
III) Calcul de la température de la surface des planètes telluriques du
système solaire
III-0) Définitions
On rappelle succinctement quelques définitions:
Corps noir : corps ne réfléchissant pas la lumière incidente, mais absorbant tous les rayonnements. Ainsi à l'équilibre
thermique, si sa température ne varie pas au cours du temps, il absorbe et réemet tous les rayonnements incidents.
Loi de Planck : indique quelle est l'énergie en fonction de la longueur d'onde du rayonnement émis par un corps noir.
Le résultat ne dépend que de la température: le spectre du rayonnement d'un corps noir ne dépend pas du rayonnement
incident.
Loi de Wien : il s'agit d'une conséquence de la loi de Planck. Elle indique pour quelle longueur d'onde, l'énergie émise
par un corps noir est maximale :
Loi de Stéfan : il s'agit également d'une conséquence de la loi de Planck. En sommant l'énergie du rayonnement émis
par un coprs noir à toutes les longueurs d'onde, il vient que l'énergie totale émise par un corps noir, par unité de surface
et de temps s'écrit : . Ainsi l'énergie émise par un corps noir ne dépend que de sa
température.
Surface d'une sphère : 4*pi*R2
Surface d'un disque : pi*R2
III-1) Pour quelle longueur d'onde l'énergie émise par la Terre et le soleil est
maximum ? On rappelle que la température de la surface du soleil est de 6000 K.
III-2) Calcul de la température de surface d'une planète sans atmosphère
a) A l'aide de la loi de Stéfan, indiquez quelle est l'expression de la puissance émise par le soleil.
b) On se place à une distance D du soleil. Indiquez quelle est la puissance par unité de surface reçue du soleil. On
supposera que les rayons du soleil arrivent perpendiculairement à nous.
c) Vue depuis le soleil, la Terre apparaît comme un disque de rayon Rt. Quelle est la puissance totale reçue par la Terre
(on demande une expression littérale sans application numérique) ?
d) En déduire l'énergie du soleil reçue sur Terre par unité de surface.
e) En supposant que la Terre est un corps noir, et en appliquant la loi de Stéfan, indiquez l'expression de la température à
la surface d'une planète en fonction de la distance au soleil.
f) On suppose à présent que la planète a un albédo A. Ainsi, si E est l'énergie reçue du soleil par unité de surface, la
planète réfléchit une énergie A*E vers l'espace. Ecrire l'expression de la température à la surface d'une planète en

fonction de la distance au soleil, en tenant compte de son albédo A.
g) Application numérique : les planètes telluriques ont un albédo A=0.07, sauf la Terre qui a un albédo de 0.3
Calculez les température de surface de Mercure, Vénus, la Terre (avec un albédo de 0.07 et 0.3) et Mars. On donne :
Rayon du soleil Rs=0.7e6 km
La température à la surface du soleil Ts = 6000 K
La distance de Mercure, Vénus, la Terre et Mars au soleil : 56, 108, 150 et 227 millions de kilomètres.
h) Les températures de surface de Mercure, Vénus, la Terre et Mars sont en réalité de 442 K, 735K, 15K et 210 K.
Comparez avec vos résultats. Que pouvez vous en déduire sur l'atmosphère de chacune de ces planètes ?
i) bonus : la distance Terre-Soleil varie entre 147 et 152 millions de kilomètres. Quelle est la variation de température
associée à ce changement de distance ? On prendra A=0.3.