Exercices charge et decharge du condensateur

1
1EXERCICE : CHARGE ET DECHARGE DU CONDENSATEUR
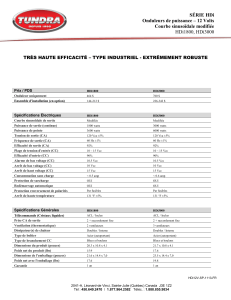
On considère le montage suivant dans lequel depuis un temps très long, l’interrupteur K1 est ouvert et
l’interrupteur K2 est fermé.
+
+
K1K2
E
R1R2
Vcc
C
v1
v2
2 kΩ20 kΩ
10 nF
2 V
5
V
AB
D
Figure 1
1. Donner dans ces conditions le schéma du montage et en déduire la valeur des tensions v1o et v2o du
schéma de la figure 1.
A l’instant t = 0, on ferme K1 et simultanément on ouvre K2.
2. Donner le schéma du montage. Quelles sont les valeurs des tensions v1i et v2i aussitôt cette
opération ?
3. Comment évoluent ensuite ces tensions ?
a) Déterminer les valeurs limites qui peuvent êtres atteintes et la constante de temps τ1 de
l’évolution.
b) Donner l’expression de la tension v1 (t) et en déduire celle de v2 (t).
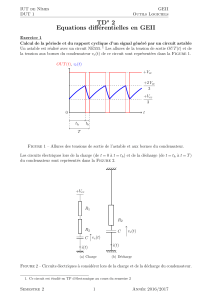
c) Tracer soigneusement leur courbe représentative sur le graphe.
4. Déterminer l’instant t1 au bout duquel la tension v1 (t) atteint zéro volt.
Sans attendre que l’évolution de v1 (t) soit terminée, à l’instant t1 où la tension v1 (t) atteint zéro volt,
le dispositif ouvre K1 et simultanément ferme K2.
5. Le temps t1 est la nouvelle origine du temps.
Examiner comment les tensions v1 (t) et v2 (t) évoluent. Donner le schéma, les équations et tracer
les courbes représentatives à la suite des graphes précédents.
1 © Ph. ROUX 2005 http://rouxphi3.perso.cegetel.net

2
-6
-4
-2
0
2
4
6
0 50 100 150 200 250 300
tension (V)
temps (microseconde)

3
CORRECTION
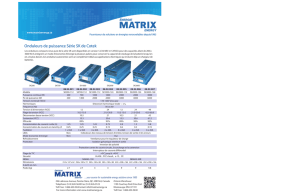
Q1 : Schéma du montage :
+
+
K2
E
R1R2
Vcc
C
v1
v2
2 kΩ20 kΩ
10 nF
2 V
5 V
AB
D
Le condensateur C est chargé sous une tension v1o de 3V alors que v2o = 2 V.
Q2 : Schéma du montage :
+
R1R2
Vcc
C
v1
v2
2 kΩ20 kΩ
10 nF 5 V
AB
D
Lors de l’événement, fermeture de K1 et ouverture de K2, le condensateur garde ses charges, autrement
dit sa tension ne peut pas évoluer instantanément. Dans ces conditions : v1i = 3 V et v2i = - v1i = - 3 V.
Q3a : On remarquera que la résistance R1 qui vient en parallèle avec VCC ne participe pas à l’évolution
des tensions v1 et v2.
Lorsque C sera complètement chargé pour t infini, son courant sera nul alors v1infini = - VCC = -5V. La
constante de temps d’évolution de la tension est telle que : τ1 = R2.C = 200 µS.
Q3b :
vt t
1
1
58( ) exp( )=− + −
τ
vt vt
21
() ()=−

4
Q3c : On notera qu’à l’instant t = 0, la tension v2 (0) passe de la valeur 2V à – 3 V.
0 1 10 4210 4310 4410 4510 4610 4710 4810 4910 40.001
6
4
2
0
4
6
5
5
t
2
v1 (t)
v1 (t)
v2 (t)
Q4 : La tension v1 (t) passe à zéro volt pour t1 = 94 µs.
Q5 :
+
+
K2
E
R1R2
Vcc
C
v1
v2
2 kΩ20 kΩ
10 nF
2 V
5 V
AB
D
La tension v2 passe instantanément à 2V.
A l’instant t = 0 le condensateur garde ses charges aussi v1ini = 0 V.
• La constante de temps est telle que : τ2 = R1.C = 20 µs.
• La tension v1infinie s’établit à 3 V.
vt t
1
2
31( ) ( exp( ))=− −
τ

5
0 1 10 52 10 53 10 54 10 55 10 56 10 57 10 58 10 59 10 51 10 4
0
1
2
3
t
v1 (t)
v2 (t)