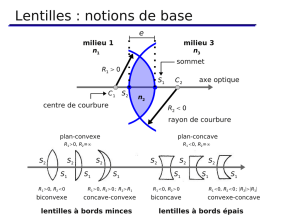
Image d`un objet par une lentille sphérique mince divergente

Chapitre X page X-1
X. IMAGE D’UN OBJET
PAR UNE LENTILLE SPHERIQUE MINCE
DIVERGENTE
Nous reprenons l’étude du chapitre précédent, mais avec une lentille divergente1 afin de voir ce qui
les différencie des lentilles convergentes. Il s’agit aussi de consolider les connaissances déjà
rencontrées.
A. Analyse qualitative de l’image d’un objet ponctuel
Sur l’axe optique, deux points, le foyer objet et le centre optique, jouent un rôle particulier pour
la position des objets2.
Les positions d’un objet par rapport à une lentille divergente se
classent donc en trois catégories : avant la lentille, entre la lentille et le
foyer objet, et enfin après le foyer objet (voir la figure 10.1). Ce
classement fait apparaître trois cas particuliers : à l’infini, sur la
lentille et au foyer objet.
Nous allons commencer par un objet situé à l’infini sur l’axe, puis nous allons le rapprocher de la
lentille, ensuite considérer un objet virtuel3 situé entre la lentille et le foyer objet et enfin
terminer par un objet virtuel situé après le foyer objet.
1 Pour l’action d’une lentille divergente sur les faisceaux lumineux, voir le chapitre VII Les lentilles sphériques,
paragraphe C.3.
2 Pour la définition des foyers image et objet voir le chapitre VIII Foyers des lentilles sphériques minces,
paragraphes C.1.a et C.2.a.
3 Sur les notions de réalité et de virtualité, voir le chapitre V Formation des images dans l’exemple du miroir
plan, paragraphe A.3.a et le chapitre VIII Foyers des lentilles sphériques minces, paragraphe F.
OF
F'
fig. 10.1 : les points
particuliers sur l'axe optique

Chapitre X page X-2
1. Objet situé à l’infini sur l’axe
Le faisceau de rayons parallèles est transformé en un
faisceau divergent. L’image est au foyer image et elle est
virtuelle. Voir la figure 10.2.
2. Objet réel
Partant de l’infini, nous rapprochons maintenant l’objet de la lentille.
Comparons les figures 10.2 et 10.3. Le
faisceau incident, qui était parallèle sur la
figure 10.2, devient divergent sur la figure
10.3. Le faisceau émergent, qui divergeait en
semblant provenir de F’, devient encore plus
divergent.
Conclusion : un objet réel donne une image virtuelle située entre le foyer image et la lentille.
3. Objet situé sur la lentille
Lorsque l’objet est situé en O, les rayons lumineux convergeant au
centre optique ne sont pas déviés, donc l’image est, elle aussi, située
en O. Voir la figure 10.4.
O F
A
8
F'
fig. 10.2 : objet situé à l'infini sur l'axe
O F
AF' A'
fig. 10.3 : objet réel
O
F' F
AA'
fig. 10.4 : objet situé
sur la lentille

Chapitre X page X-3
4. Objet virtuel situé entre la lentille et le foyer objet
Nous considérons maintenant un faisceau convergent
frappant la lentille. Il émerge en un faisceau moins
convergent. Voir la figure 10.5.
Conclusion : un objet virtuel situé entre la lentille et le foyer objet donne une image réelle.
5. Objet virtuel situé au foyer objet
L’image est à l’infini sur l’axe. Le faisceau convergent est
transformé en un faisceau de rayons parallèles. Voir la figure
10.6.
6. Objet virtuel situé après le foyer objet
Partant du foyer objet, éloignons encore l’objet de
la lentille. Comparons les figures 10.7 et 10.6 :
Puisque sur la figure 10.6 le faisceau convergeant
vers F émerge en un faisceau parallèle, sur la
figure 10.7 un faisceau moins convergent émerge
en divergeant.
Les prolongements des rayons émergents se
coupent en avant de la lentille.
Conclusion : un objet virtuel situé après le foyer objet donne une image virtuelle.
O FAF' A'
fig. 10.5 : objet virtuel situé entre la lentille
et le foyer objet
O F
F' A'
8
fig.10.6 : objet virtuel situé
au foyer objet
O FF'A' A
fig. 10.7 : objet virtuel situé après le foyer objet

Chapitre X page X-4
7. Conclusion
Un objet réel donne une image virtuelle.
Un objet virtuel situé entre la lentille et le foyer objet donne une image réelle.
Un objet virtuel situé après le foyer objet donne une image virtuelle.
Un objet situé à l’infini donne une image virtuelle située au foyer objet.
Un objet virtuel situé au foyer objet donne une image située à l’infini.
Remarque : Comme nous pouvions nous y attendre, cette étude donne des résultats différents de
ceux des lentilles convergentes. En particulier, les images sont virtuelles sauf lorsque l’objet est
situé entre la lentille et le foyer objet (en mettant à part le cas de l’image à l’infini).
B. Etude quantitative des deux cas objet ou image à l’infini
1. Objet étendu situé à l’infini
a) La situation
La situation est la même que pour une lentille convergente. Il s’agit de décrire un objet étendu
situé à l’infini, peu importe la nature du système optique.
b) Schéma : figure 10.8.
c) Position de l’image
L’objet étant à l’infini, son image est dans le plan focal image.
d) Taille de l’image
Sur la figure 10.8, dans le triangle OF’B’ rectangle en F’, nous calculons :
' ' 'tan tan 'tan
B B B
F B OF f f
.
' ' tan 'tan
BB
F B f f
L’image est virtuelle et droite. (L’angle
B est positif ainsi que
''FB
.)
OF
F'
B'
A
8
B
8
B
fig. 10.8 : objet étendu situé à l'infini

Chapitre X page X-5
Remarque : Dans le cas du Soleil et des planètes l’angle
B est faible, donc tan B  B (exprimé en
radian), alors :
''FB
 -f ’
B.
2. Image étendue située à l’infini
a) Construction
L’objet étendu est alors virtuel et situé au foyer objet (voir la figure 10.9).
Le faisceau incident convergeant virtuellement vers A n’est pas tracé sur la figure pour ne pas la
brouiller. Ce faisceau incident émerge en un faisceau parallèle à l’axe formant l’image A’.
Le faisceau incident convergeant virtuellement vers B émerge en un faisceau parallèle formant
l’image B’. Chaque point FS de l’objet donne une image située à l’infini dans la direction ’ que
fait l’axe secondaire (FSO) avec l’axe optique. L’image est formée d’un ensemble de faisceaux
parallèles déterminés par des angles ’ compris entre 0 et ’B.
b) Position de l’image
L’objet étant au foyer objet, son image est à l’infini.
c) Rayon angulaire de l’image
La taille de l’image est de toute façon infinie. Son étendue est caractérisée par son rayon
angulaire ’B . Sur la figure 10.9, dans le triangle OFB rectangle en F, nous calculons :
tan 'BFB
FO
.
L’image est renversée, ce qui se traduit par ’B < 0 :
tan ' '
BFB FB
FO f
O
'BF A
BB'
8
A'
8
fig. 10. 9 : objet étendu situé au foyer objet