Télescope de Newton

Spécialité Physique Télescope de Newton Chap.2
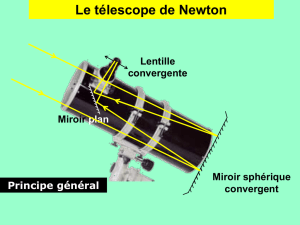
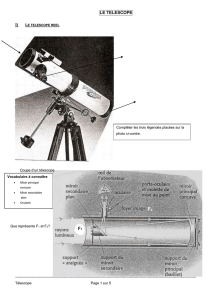
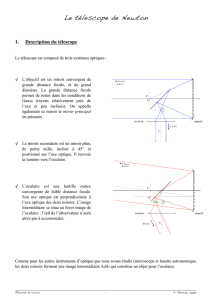
I. Description du télescope de Newton
Le télescope a pour rôle de former l’image d’un astre par
réflexion (d’où le nom d’instrument « réflecteur »
contrairement à la lunette astronomique appelée instrument
« réfracteur » ). La surface réfléchissante constituant l’objectif
est en fait parabolique, mais le miroir sphérique en fournit une
bonne approximation.
Le faisceau lumineux revenant sur lui-même dans le
télescope, il faut placer l’oculaire de façon que l’observateur
ne perturbe pas le faisceau incident ; il existe plusieurs
dispositifs auxquels sont associés des noms de télescopes.
Dans le télescope de Newton, un miroir plan, incliné à 45°,
permet de renvoyer latéralement le faisceau lumineux réfléchi
par le miroir objectif pour que l’image finale se forme à
l’extérieur du tube du télescope.
II. Formation des images
Hypothèse : l’objet
AB
observé est situé à
l’infini, vu sous l’angle θ, le point A étant sur
l’axe du miroir.
Principe de construction :
➢Le miroir principal donne de l’objet
AB
une image A1B1 ;
➢L’image A1B1 sert d’objet pour le miroir
plan qui en donne une image A2B2 ;
➢L’image A2B2 sert d’objet pour l’oculaire qui donne une image définitive A’B’ à l’infini vue sous un angle .
02/01/12 P02_Telescope_Newton.odt 1/3

III. Grossissement G
L’angle θ sous lequel on voit l’objet à l’œil nu est aussi l’angle sous lequel on voit l’image A1B1 depuis le point D
Hypothèse : θ petit donc tan θ ≈ θ =
A1B1
DB1
=
A1B1
f ' 1
Dans le cas d’une vision à l’infini, télescope afocal, l’angle θ’ sous lequel on voit l’image A’B’ est aussi l’angle
sous lequel on voit l’objet A2B2 depuis le centre de l’oculaire : θ’ =
A2B2
O2A2
=
A2B2
f '2
A2B2 est l’image de A1B1 donnée par le miroir plan. Cette image symétrique de l’objet par rapport au miroir. Elle a
donc même dimension : A2B2 = A1B1 d’où θ’ =
A2B2
f '2
=
A1B1
f ' 2
Par définition, G =
θ '
θ
=
A1B1
f ' 2
×
f ' 1
A1B1
soit G =
f '1
f '2
Dans le cas d’une vision à l’infini (télescope afocal), le grossissement est égal au quotient de la distance focale du
miroir principal par celle de l’oculaire.
IV.Cercle oculaire
Le cercle oculaire est l’image du miroir principal donné par l’oculaire. L’œil doit être placé à son niveau pour
recevoir le maximum de lumière.
Pour construire le cercle oculaire, il faut d’abord construire l’image du miroir principal donnée par le miroir
secondaire puis cette image sert d’objet pour l’oculaire qui en donne le cercle oculaire.
On peut retrouver la position du cercle en utilisant la formule de conjugaison appliquée à l’oculaire.
➢Le télescope est afocal donc
O2A2
=
f ’2
;
A2
est le symétrique de
A1
par rapport au miroir plan donc
OA2
=
OA1
;
SA1
=
f ’1
=
SO
+
OA1
=
SO
+
OA2
d’où
SO
+
OO2
=
SO
+
OA2
+
A2O2
=
f ’1
+
f ’2
.
➢Pour un télescope afocal ,
SO
+
OO2
=
f ’1
+
f ’2
.
V. Avantages du télescope sur la lunette astronomique
L’objectif étant de type réflecteur, les pertes de lumière sont moins importantes que dans une lunette.
De plus, il est facile de fabriquer des miroirs de grand diamètre que de grandes lentilles.
Le télescope est donc un meilleur collecteur de lumière que la lunette
VI. Construction graphique de l’image intermédiaire et de l’image définitive d’un objet à l’infini données par le
télescope de Newton ; Position du cercle oculaire : Voir page 4
AB objet situé à l’infini.
A1B1
image de AB donnée par le miroir sphérique (
M1
) : elle se forme au foyer F de ce miroir.
A2B2
image de
A1B1
donnée par le miroir plan (
M2
) : c’est le symétrique de
A1B1
par rapport au plan de ce
miroir ; elle se situe dans le plan focal objet de la lentille (L).
A’B’ image de
A2B2
donnée par la lentille (L) ; elle se situe à l’infini.
VII. Modélisation d’un télescope de Newton
On réalise un télescope de Newton à l’aide d’un miroir sphérique concave de 10 cm de distance focale et 4,0 cm de
diamètre, d’un miroir plan et d’une lentille convergente de 2,0 cm de distance focale.
Le centre du miroir secondaire est situé sur l’axe optique du télescope à 2,0 cm du foyer du miroir principal. On
observe, à l’aide de ce télescope, un objet AB situé à l’infini, A étant sur l’axe du télescope. Le miroir principal
donne de cet objet AB une image
A1B1
de 8,0 mm de hauteur.
1) Faire un schéma à l’échelle 1/1 sur lequel seront représentés les deux miroirs, la lentille oculaire et l’image
A1B1
2) Tracer un des rayons qui permettent de construire l’image
A1B1
et en déduire l’angle θ sous lequel est vu l’objet
AB depuis le lieu d’observation.
3) Construire l’image
A2B2
donnée par le miroir plan ainsi que l’image définitive A’B’.
4) Calculer l’angle θ’ sous lequel est vue l’image A’B’ et en déduire le grossissement du télescope.
5) Vérifier que ce grossissement est bien égal au rapport de la distance focale de l’objectif à celle de l’oculaire.
6) Tracer la marche d’un rayon quelconque issu de B.
7) Quelle est la distance minimale qui doit séparer le centre du miroir secondaire du foyer du miroir primaire ? De
quoi dépend-elle ?
VIII. Exercice 22 p 42
02/01/12 P02_Telescope_Newton.odt 2/3