Circuit logique

A. Dipanda - circuits combinatoires 1
Circuit logique
Circuit logique
I
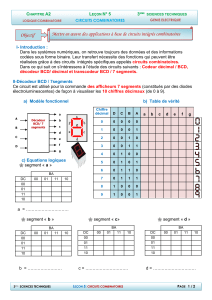
IDéfinition
Définition
•Un circuit logique est un dispositif électronique
permettant la réalisation d’une fonction logique
•
•Chaque variable de la fonction est matérialisée Chaque variable de la fonction est matérialisée
par un conducteur et sa valeur sera définie à partir
par un conducteur et sa valeur sera définie à partir
de sa tension.
de sa tension.
Entrées {
 }Sorties
masse

A. Dipanda - circuits combinatoires 2
Circuit logique
Circuit logique
•
•Les entrées et sorties Les entrées et sorties
– Circuit logique↔f(x1, x2, x3,..., xn) →(y1, y2, y3,..., ym)
entrées sorties
– Les entrées sont les conducteurs qui vont permettre de
présenter les opérandes.
– Les sorties sont les conducteurs qui vont permettre de
consulter le résultat.

A. Dipanda - circuits combinatoires 3
Circuit logique
Circuit logique
Iles conducteurs sont appelés des broches ; il
en existe 4 types :
•entrées “ normales ” : forçées par l’utilisateur
•sorties “ normales ” : forçées par le circuit
•sorties 3 états : (peuvent être laissées libres dans
certains cas) on les utilise quand on travaille avec
les bus, circuit à validation.
•les collecteurs ouverts : libres ou forçés à 0

A. Dipanda - circuits combinatoires 4
Circuit logique
Circuit logique
IAssemblages de circuits logiques
règles ou principes à respecter :
– compatibilité des tensions entre les entrées et les sorties
– à un instant donné, on ne peut forçer une entrée que
d’une seule façon
f
g

A. Dipanda - circuits combinatoires 5
circuit combinatoire
circuit combinatoire
I
IIntroduction
Introduction
•un circuit combinatoire réalise sur ses sorties une
fonction de ses entrées : s=f(e)
•Un circuit combinatoire n’a pas de mémoire
interne.
•il y a toujours un moment de latence entre le
moment où on envoie quelque chose en entrée et
le moment où on récupère quelque chose en
sortie ; cet intervalle de temps est connu et
s’appelle le “ délai de propagation ” , noté tp.