D.S.T. N° 2

CLASSE DE PREMIÈRE S Le : 13 novembre 2013
Durée : 1 h 30
Physique-Chimie
DEVOIR SUR TABLE N° 2
TOUT DOCUMENT INTERDIT.
L’usage de calculatrices scientifiques à mémoire est autorisé.
Les résultats numériques doivent être précédés d’un calcul littéral.
La présentation et la rédaction font partie du sujet et interviennent dans la notation.
L’épreuve est notée sur 16 points auxquels s’ajouteront les points d’épreuve pratique sur 4 points.
I ] Optiquez-moi… (sur 6,50 points)
A] Myopie.
Un œil myope a un cristallin trop convergent : lorsqu'il regarde un objet à l'infini, l'image se forme à 0,500 mm devant
la rétine, laquelle se trouve à 15,2 mm du cristallin. Pour l’œil sans défaut optique, en revanche, l'image se forme sur la
rétine pour tout objet placé entre 25,0 cm et l'infini, qui est l'ensemble des positions d'objet que peut voir cet œil.
1. Calculer la distance focale du cristallin de l'œil myope au repos.
2. En déduire la vergence correspondante. Est-elle minimale ou maximale pour cet œil myope ? Justifier.
3. Quelle est la vergence du cristallin lorsque l'œil myope observe un objet à 25,0 cm, l'image étant formée sur la rétine ?
4. En supposant que l'œil myope puisse augmenter sa vergence de 4,00 δ s'il accommode au maximum, montrer qu'un
myope peut voir net un objet situé à moins de 25,0 cm du cristallin. Ainsi, sans lunettes de correction, un œil myope
voit mieux de près qu'un œil sans défaut.
B] Cache-cache.
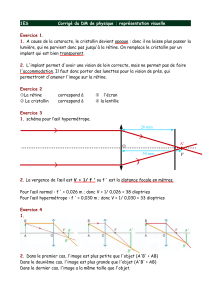
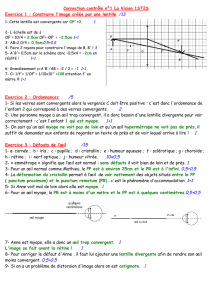
Un objet lumineux en forme de croissant (voir Figure ci-
contre) est modélisé par ses points extrêmes A et B. Sa taille
est : AB = 4,0 cm. Cet objet est placé à 30 cm d'une lentille de
vergence : C = + 5,0 δ et de diamètre : D = 6,0 cm. Soient I, J,
K, O, L, M et N des positions de haut en bas sur le diamètre de
la lentille espacées d'un centimètre. L'image obtenue de l’objet
AB est recueillie sur un écran.
1. Déterminer la distance focale f ' de cette lentille.
2. Déterminer la taille et la position de l'image A'B' de AB
par construction graphique, sur l’annexe millimétrée.
Échelle pour la représentation graphique :
sur l'axe horizontal : 1 cm représente 6 cm ; sur l'axe vertical : 1 cm représente 2 cm.
3. Un cache noir est placé sur la moitié haute de la lentille (voir Figure ci-contre). Prévoir ce qui est
vu sur l'écran.
4. Tracer, sur le schéma de la question 2., les rayons issus de A puis de B passant par les points I,
J, K, L, M, N et O une fois le cache placé.
5. Déduire de la construction graphique, ce qui est observé sur l'écran.
6. Cette conclusion est-elle conforme à la prévision de la question 3. ?
II ] Synthèses des couleurs. (sur 3,25 points)
1. Une lumière blanche, obtenue à l’aide de trois spots lumineux respectivement rouge (700 nm), vert (546,1 nm) et bleu
(435,8 nm) traverse un filtre coloré. Remplir le tableau suivant, en fonction de la nature du filtre utilisé. On justifiera les réponses.
Filtre utilisé Couleurs des radiations
absorbées Couleur transmise perçue
Aucun
Cyan
Magenta
Jaune
Rouge
Bleu
Vert
Cyan + Magenta + Jaune
... / ...

2. Un ou plusieurs spots de lumière colorée éclairent une même zone d’un écran blanc. De quelle couleur la lumière
diffusée par l’écran est-elle perçue ? On complétera le tableau suivant en justifiant les réponses.
Spot Couleur diffusée
Spot bleu (435,8 nm) + spot rouge (700 nm)
Spot bleu (435,8 nm) + spot vert (546,1 nm)
Spot vert (546,1 nm) + spot rouge (700 nm)
Spot vert (546,1 nm) + spot rouge (700 nm) + Spot bleu (435,8 nm)
Aucun spot
On donne :
III ] Sources de lumières. (sur 6,25 points)
A] Température et rayonnement.
1. Énoncer la loi de Wien.
2. Tracer l’allure de la courbe de l’intensité lumineuse : I = f (λ) du rayonnement d’un corps noir chauffé à la
température T.
3. Quelle est la température d’un corps noir dont la longueur d'onde d'émission lumineuse maximale se situe à 300 nm ?
4. Quelle est la température d’un corps noir dont la longueur d'onde d'émission lumineuse maximale se situe à 1,00 µm ?
5. Dans quel domaine de longueurs d'onde se situe le maximum d'énergie rayonnée par le corps humain, de
température : θ = 37,0°C ?
On donne : constante de Wien : σ
σσ
σWien = 2,898.10–3 uSI.
B] Niveaux d’énergie de l’atome d’hydrogène.
Le diagramme d'énergie ci-contre représente les différents niveaux accessibles pour
les électrons d'un atome d'hydrogène. Ces niveaux sont représentés par des lignes
horizontales.
1. Quelle énergie faut-il apporter à l'atome d’hydrogène pour que son électron passe de
la couche (K) à la couche (N) ? Exprimer cette énergie en électronvolts, puis en joules.
2. Quelle doit être la fréquence ν
νν
ν de la radiation qui permet cette transition ?
3. Une radiation de fréquence ν
νν
ν’ = 2 ν
νν
ν peut-elle être absorbée par cet atome ? Justifier.
4. 4.1. Quelles transitions électroniques sont envisageables lorsque l'électron est sur la
couche (N) et se désexcite totalement ?
4.2. Déterminer les valeurs des longueurs d’onde correspondant à ces transitions.
4.3. À quel domaine d’onde chaque radiation associée appartient-elle ?
On donne : Célérité de la lumière dans le vide : c = 3,00.108 m.s-1.
Constante de Planck : h = 6,63.10–34 J.s. 1 eV = 1,60.10–19 J.
.../ p. 3

Première S Devoir sur Table N° 2 Page 3
ANNEXE MILLIMÉTRÉE
À rendre avec la copie en indiquant son NOM :
EXERCICE I ] B] 2.