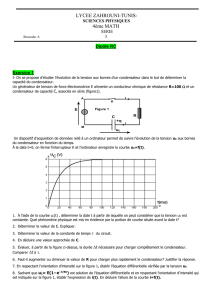
Les Condensateurs

Les Condensateurs
Première partie
Généralités
La charge d 'un condensateur
Association
un peu de théorie théorique...
Un condensateur est assimilable à deux plaques disposées face à face. En règle générale on pourra
dire qu’un condensateur est constitué de deux conducteurs séparés par un isolant (appelé également
diélectrique), cet isolant peut être l’air ambiant par exemple.
Le symbole du condensateur
Lorsque l’on applique une tension aux bornes d’un condensateur celui-ci se charge et conserve une
quantité d’électricité (Q), proportionnelle à la tension appliquée. Cette quantité d’électricité est en
fait de l’énergie emmagasinée, celle- ci sera restituée lorsque le condensateur se déchargera.
Le condensateur est donc un réservoir d’énergie qui se remplie ou se vide.

Un condensateur est caractérisé par sa capacité, celle-ci est exprimée en FARAD, 1 FARAD
correspond à une charge emmagasinée de 1 Coulomb sous une tension d’alimentation de 1 Volt.
Q = CU
C en farad
Q en coulomb
U en volt
Plus cette capacité est importante et plus le condensateur pourra emmagasiner d ' énergie
W = 1/2 CU²
W en joules
C en farad
U en volt
la capacité s' exprime selon la formule ci après elle dépend :
de la surface des deux armatures en regard ( S en mètre carré )
de l 'épaisseur du diélectrique qui sépare les armatures ( e en mètre )
de la nature du diélectrique ( epsilon r est une constante qui dépend du matériau utilisé ) , voir
tableau 1
de la permittivité du diélectrique par rapport au vide ( epsilon 0 )
C est exprimé en FARAD . Le FARAD est une très grande unité , on utilisera des sous multiples pour
exprimer la capacité d 'un condensateur , par exemple le milliFarad (MF ), le micro Farad ( µF ) , le
nanoFarad ( nF) , le picofarad ( pF )
8.85 x10 -12 est un coefficient ( issu de epsilon 0 )

Tableau des permittivités ( r ) selon les matériaux utilisés en diélectrique
Tableau 1
Selon la résistance incorporée dans le circuit un condensateur se chargera et se déchargera plus ou
moins vite , le produit RxC ( la résistance multiplié par le condensateur ) se nomme constante de
temps ( Tau ).
T = RC
T en seconde
R en ohm
C en farad
Sur la figure 1 on connecte un condensateur (ici deux plaques métalliques en regard) à une pile de
4.5 V. Un interrupteur permet de mettre en service le montage, un ampèremètre mesure le courant
circulant dans le circuit. Une résistance insérée dans le circuit permet de limiter le courant.
L’interrupteur est ouvert, aucun courant ne circule dans le circuit, aucune charge électrique n’est
présente sur les armatures.
Figure 1

Sur la figure 2 on ferme l’interrupteur, que se passe t’il ?
Des charges électriques du pôle + de la pile vont s’accumuler sur la plaque (armature) rouge sur
notre
schéma et des charges négatives vont s’accumuler sur l’armature négative (bleue sur le schéma).
L’ampèremètre est chargé de mesurer le nombre d’électron passant par seconde dans le circuit, il va
dévier indiquant que des charges électriques se déplacent.
Figure 2
Sur la figure 3 l’interrupteur est toujours fermé, mais il n’y a plus de courant circulant dans le circuit,
on dit alors que le condensateur est chargé, il y a autant de charges sur l’armature positive que sur
l’armature négative.
Figure 3

La charge d’un condensateur n’est pas linéaire, elle décrit une courbe.
Sur cette courbe nous pouvons faire plusieurs remarques :
Il y aura toujours 63% de la tension d’alimentation aux bornes du condensateur à 1 T c’est à dire à
une fois le produit RC.
exemple : C= 1000 µF, la résistance R = 50000 ohm et la tension d’alimentation = 12 V
alors à T = RC = (50000) x (1000 x 10 -6) = 50 secondes
cela veut dire que dès que l’on a connecter le condensateur à la tension de 12V via la résistance 50
secondes après on aura 63% de 12 V, c'est à dire 7.56 V aux bornes du condensateur.
Il y aura toujours 95% de la tension d’alimentation aux bornes du condensateur à 3 T c’est à dire à
trois fois le produit RC.
exemple : C= 1000 µF , la résistance R = 50000 ohm et la tension d 'alimentation = 12 V
alors à 3T = 3RC = (50000) x (1000 x 10 -6 ) x 3 = 150 secondes
cela veut dire que dès que l 'on a connecter le condensateur à la tension de 12V via la résistance 150
secondes après on aura 95% de 12 V , c'est à dire 11.4 V aux bornes du condensateur.
Il y aura toujours 99% de la tension d’alimentation aux bornes du condensateur à 5 T c’est à dire à
cinq fois le produit RC.
exemple : C= 1000 µF , la résistance R = 50000 ohm et la tension d 'alimentation = 12 V
alors à 5T = 5RC = (50000) x (1000 x 10 -6 ) x 5 = 250 secondes
cela veut dire que dès que l 'on a connecter le condensateur à la tension de 12V via la résistance 250
secondes après on aura 99% de 12 V , c'est à dire 11.88 V aux bornes du condensateur.
On peut dire qu 'un condensateur est complètement chargé entre 3 et 5 Tau ( RC ) et ceci