l`atome et la mecanique de newton

Karine Vasseur - TSC4 – 2005 - 2006
1
L'ATOME ET LA MECANIQUE DE NEWTON
OUVERTURE AU MONDE QUANTIQUE
I. LIMITES DE LA MECANIQUE DE NEWTON : QUANTIFICATION DE L'ENERGIE
1. Interactions au niveau de l'atome
Un atome est constitué d'un noyau et d'électrons qui gravitent autour.
Les électrons et le noyau subissent en même temps :
• L'interaction gravitationnelle du fait de leur masse : FG= - G r
2u
r
m' m.
r
• L'interaction électrostatique du fait de leur charge : Fe= k r
2u
r
q' q. r
Si on calcule le rapport F
F
G
e, on trouve F
F
G
e≈ 2,3.1039 : à l'échelle atomique, c'est l'interaction
électrostatique qui prédomine et qui assure la cohésion de l'atome.
2. Confrontation expériences/théorie classique et quantification de l'énergie
Au 19ème siècle, de nombreuses expériences ont été menées sur l'atome comme l'effet photoélectrique.
Lorsqu'on éclaire une plaque métallique (émetteur) avec une source lumineuse de fréquence ν variable,
on constate que pour une valeur de ν appelée fréquence seuil νS, on observe la circulation d'un courant
électrique dans un circuit constitué de la plaque métallique et d'un autre plaque appelée collecteur.
Cette intensité est d'autant plus grande que la puissance lumineuse est grande.
La mécanique classique ne permet pas, entre autres, d'expliquer l'existence d'une fréquence seuil νS.
Afin d'expliquer l'effet photoélectrique, Einstein a proposé en 1905 que les échanges d'énergie entre
le rayonnement lumineux et la matière étaient quantifiés : il parle de quanta (petits paquets) de
lumière.
Planck avait déjà introduit cette idée de quantification de l'énergie (1900) lorsqu'il fallut expliquer le
rayonnement du corps noir.
Enfin, d'autres expériences avaient montré que les rayons des atomes dépendent du numéro atomique.
L'énergie d'un atome ne peut prendre que des valeurs discrètes : on dit qu'elle est quantifiée.
II. SPECTRES ATOMIQUES
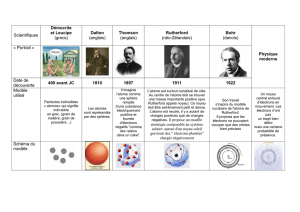
1. Modèles de l'atome
La notion d'atome a mis longtemps à percer. Dès l'antiquité, Démocrite parla d'atome (indivisible) mais
cette notion fut remise en question pendant de très nombreuses années.
Au 19ème siècle, Dalton réintroduit la notion d'atome afin d'expliquer les propriétés chimiques de
certains mélanges.
Parallèlement à la découverte de l'électron (fin du 19ème siècle), la connaissance de la structure de
l'atome s'établit progressivement.
Plusieurs modèles furent proposés :
• Modèle de Thomson, dit de l'atome fourré aux électrons, où les électrons sont entourés de charges
positives ;
• Modèle de Rutherford, dit modèle planétaire, suggéré par Jean Perrin, dans lequel les électrons
gravitent autour d'un volume chargé positivement.
L'expérience menée par Rutherford en 1911 afin de tester la répartition des charges à l'intérieur d'un
atome détruisit le modèle de Thomson.

Rutherford émit l'hypothèse que les électrons sont soumis à l'attraction du noyau suivant une force
électrostatique de Coulomb, tout comme les planètes sont attirées par le Soleil.
Cependant, ce modèle "planétaire" ne permettait pas d'expliquer pourquoi les orbites des électrons à
l'intérieur de l'atome ne pouvaient prendre que des valeurs discrètes et pourquoi les spectres
d'émission des atomes comme l'hydrogène étaient discontinus.
Bohr proposa en 1913 une amélioration du modèle de Rutherford en y adjoignant une condition de
quantification des orbites des électrons.
Bohr imposa que les orbites des électrons étaient circulaires et correspondaient à des niveaux
d'énergie bien définis. Enfin, leur rayon ne pouvait prendre que des valeurs discrètes.
Depuis, le modèle de l'atome a évolué vers une interprétation probabiliste dont les précurseurs sont
Heisenberg et Schrödinger (notion de fonction d'onde et d'équation de Schrödinger).
2. Niveaux d'énergie d'un atome
A l'intérieur d'un atome, les électrons ne peuvent occuper que des orbites (ou niveaux d'énergies)
bien définies. L'énergie associée à ses différentes orbites est négative.
A chaque niveau d'énergie, on associe un nombre n, appelé nombre quantique principal.
Il existe un niveau d'énergie le plus bas, appelé niveau fondamental E1 dans lequel se trouve
l'atome au repos. C'est l'état le plus stable. Le niveau fondamental correspond à n = 1.
Les niveaux d'énergie plus élevés que E1 sont appelés niveaux excités et correspondent à n > 1.
Lorsque l'atome est ionisé, alors son énergie est égale à 0 et correspond à n ∞.
Le passage d'un niveau d'énergie vers un autre s'appelle une transition.
La variation d'énergie ∆E entre deux niveaux d'énergie est égale à :
|∆E| = h ν = h
λ
c
où h la constante de Planck, h = 6,62.10-34 J.s, ν est la fréquence et c la célérité de la lumière
dans le vide.
Cette variation d'énergie se produit :
• lorsqu'on fournit à l'atome de l'énergie (sous forme de rayonnement): l'atome passe de son
niveau fondamental E1 vers un niveau excité. Il absorbe un rayonnement de fréquence ν.
• lorsque l'atome se désexcite: l'atome passe d'un niveau d'énergie excité vers un niveau
d'énergie plus faible (excité ou fondamental). Il émet un rayonnement de fréquence ν.
En général, les énergies sont exprimées en électron-Volt (eV).
On peut aussi parler de niveaux d'énergie pour des molécules ou des noyaux.
Dans ce cas, les énergies s'expriment plutôt en MeV pour le noyau et en dizaine d'eV pour les
molécules.
Remarque
Ce n'est qu'en 1926 que Lewis, physicien à Berkeley, a défini le photon comme le corpuscule qui
transporte l'énergie lumineuse hν.
Cette définition vient après la théorie onde-corpuscule développée par le physicien français de Broglie
dès 1922 et pour laquelle il obtint le prix Nobel de physique en 1929.
Karine Vasseur - TSC4 – 2005 - 2006
2

3. Application : l'atome d'hydrogène
C'est en voulant interpréter le spectre de l'atome d'hydrogène que Bohr a proposé son modèle.
Dans le cas de l'atome d'hydrogène, on montre que les niveaux d'énergies En s'écrivent :
En = - n
E
2
1 avec E1 = 13,6 eV
Dans ce cas, le niveau fondamental correspond à E1 = - 13,6 eV, l'état ionisé à E∞ = 0 eV.
Il faut fournir 13,6 eV pour ioniser un atome d'hydrogène. Cela correspond à l'énergie d'ionisation.
Le spectre de l'atome d'hydrogène présente des séries de raies, appelées séries de transition.
SPECTRE DE L'ATOME D'HYDROGENE
Karine Vasseur - TSC4 – 2005 - 2006
3