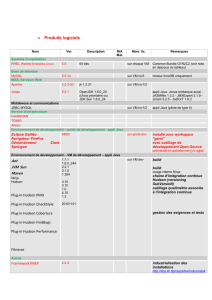
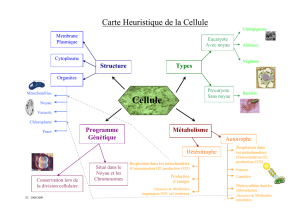
Estimation des densités de probabilité par l`algorithme plug-in

M. TROUDI (ENST Br/ ReGIM - ENIS)
1
Estimation des densités de probabilité
par l’algorithme plug-in

M. TROUDI (ENST Br/ ReGIM - ENIS)
2
Estimation des densités de probabilité :
État de l’art
Méthodes paramétriques :
Méthodes basées sur le maximum de vraisemblance
Méthodes de Pearson basées sur les moments
centrés réduits d'ordre 3 ou 4
Méthodes non paramétriques :
Méthode de l’Histogramme
Méthode du noyau
Méthode du noyau difféomorphisme
Méthode des fonctions orthogonales

M. TROUDI (ENST Br/ ReGIM - ENIS)
3
Estimateur à noyau
( Rozenblatt 1956 – Parzen 1962)
nquand
nheth
equadratiqumoyenneeneConvergenc
hXx
K
nh
xf
nn
n
in
i
n
n
0
1
1
^

M. TROUDI (ENST Br/ ReGIM - ENIS)
4
Etude asymptotique relative au pas hn
dx xffJ
h
hfJ
nh
KM
dx xfxfEffD
du uKKM
hxf
nh
KMxf
xfxfE
n
n
n
nn
n
n
n
2
4
2
^^
2
2
42
2
^
)) (''()( avec
)(
4)(
)(
),(
intégrée e quadratiqu moyenne en e Convergenc
)()( avec
4
)) (''(
)(

M. TROUDI (ENST Br/ ReGIM - ENIS)
5
Minimisation de (hn)
5
4
5
1
5
1
*)()(
5
4KMfJnh n
EQMI minimal
5
4
5
1
5
4
^
2)()(
4
5
),( KMfJnffD n