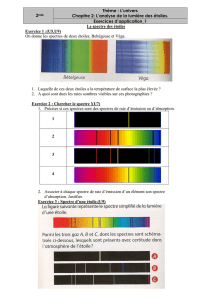
Analyse spectrale

L'analyseur de spectre
1
Analyse spectrale
1. Principe de l'analyse spectrale
Un signal se représente naturellement par sa variation par rapport au temps. C'est pourquoi on
visualise volontiers les signaux électriques à l'aide d'un oscilloscope. Le comportement d'un certain
nombre de dispositifs se décrit facilement pour un signal sinusoïdal permanent (régime
harmonique). C'est le cas, par exemple de l'oreille humaine. Il convient alors de décomposer les
signaux en signaux sinusoïdaux élémentaires. C'est le but de l'analyse spectrale. Suivant la forme du
signal, cette décomposition est plus ou moins difficile. Pour simplifier, nous envisagerons dans un
premier temps, des signaux périodiques. C'est le cas, par exemple, du signal de la figure 1.
-1,5
-1
-0,5
0
0,5
1
1,5
012345678910 11 12 13 14 15 16 17 18 19 20 21
Figure 1: Signal périodique
Ce signal est "riche" de trois composantes sinusoïdales. On appelle spectre, la représentation
des composantes suivant l'axe des fréquences (figure 2).
0 f02f03f 0f
Figure 2: Spectre du signal de la figure 1
On représente en ordonnées l'amplitude des différentes composantes du signal. Pour que
l'information soit complète, il faudrait associer à chaque raie sa phase. L'appareil qui permet de
mesurer l'amplitude des différentes composantes d'un signal est un analyseur de spectre.

L'analyseur de spectre
2
2. Analyseur de spectre
2.1. Principe de fonctionnement
Un analyseur de spectre est un appareil qui permet de visualiser directement le spectre d'un
signal. Le principe de son fonctionnement est celui représenté sur la figure 3.
Signal
Filtre
passe-bas
vidéo
Mélangeur
Filtre de
fréquence
intermédiaire
Détection
Oscillateur
local Rampe de
commande
Affichage
Filtre
passe-bas
Figure 3: Principe de fonctionnement d'un analyseur de spectre
en bande de base
2.2. Mélangeur
Le signal d'entrée, après être passé dans un filtre passe-bas, est mélangé à un signal de
fréquence variable commandé par une rampe. Si fs et fOL sont respectivement les fréquences du
signal et de l'oscillateur local, les premières fréquences qui apparaissent à la sortie du mélangeur
sont fOL+fs et |fOL-fs|. On choisit généralement la fréquence différence appelée fréquence
intermédiaire fFI.
2.3. Filtre de fréquence intermédiaire
Le filtre de fréquence intermédiaire est un filtre passe-bande. Sa largeur 2Δf est faible. Ce qui
en sort est dans la bande fFI±Δf. Cela correspond aux composantes du signal d'entrée situées dans la
bande fOL-fFI±Δf. C'est donc une fenêtre de largeur Δf que l'on balaye sur le spectre du signal à
analyser (comme lorsqu'on sélectionne une station sur un poste de radio). Ce filtre définit donc la
résolution spectrale de la mesure (Resolution band width en anglais ou RBW).
Il est courant de choisir une valeur de 2Δf très faible. Ceci peut ne pas être possible si la
fréquence intermédiaire est trop élevée. Dans ce cas, il convient d'utiliser plusieurs changements de

L'analyseur de spectre
3
fréquence successifs. La largeur du filtre peut alors être raisonnable par rapport à la dernière
fréquence intermédiaire.
2.4. Filtre d'entrée
Le filtre passe-bas à l'entrée a pour objet d'éliminer les composantes du signal d'entrée qui
pourraient intervenir dans le mélange.
Supposons par exemple que l'oscillateur local fournisse une fréquence comprise entre 3,6
GHz (fmin) et 6,5 GHz (fmax). Prenons une fréquence intermédiaire de 3,6 GHz (fFI). Si on ne
considère que la fréquence différence, on verra les composantes du signal comprises entre 0 GHz
(fmin-fFI) et 2,9 GHz et celles comprises entre 7,2 GHz (fmin+fFI) et 10,1 GHz (fmax+fFI) (à cause de
la valeur absolue). Il convient donc d'éliminer toutes les fréquences supérieures à l'aide du filtre
passe-bas d'entrée.
2.5. Amélioration du niveau de détection
Si la composante du signal à mesurer est trop faible, elle peut être noyée dans le plancher de
bruit de l'appareil. Tant que la largeur spectrale du signal est plus petite que la résolution
fréquentielle (RBW) la réduction de celle ci améliorera le rapport signal/bruit. Au-delà, les niveaux
du signal et du bruit seront réduits en même temps, et la mesure du signal deviendra non
significative.
Une amélioration du rapport signal/bruit reste cependant possible en traitant le signal après
détection. On joue alors sur les fluctuations basses fréquences résultant de la transposition de
fréquence. Deux techniques sont possibles :
• filtrer le signal "video" (en anglais Video Band Width ou VBW),
• effectuer un moyennage sur plusieurs balayages (en anglais averaging ou Video
averaging).
Dans les deux cas, l'amélioration sera obtenue au détriment du temps de mesure.
2.6. Temps de balayage
Le balayage en fréquence s'obtient par une variation de la fréquence de l’oscillateur local.
C’est en quelque sorte une forme de modulation de fréquence. Cette modulation se traduit par des
raies latérales sur le spectre du signal à la fréquence intermédiaire. Ces raies doivent apparaître
confondues avec la raie centrale à l’échelle de la bande passante du filtre. Cela signifie que plus la
bande passante du filtre est étroite, plus le balayage doit être lent. On ne peut donc pas choisir
n’importe quel balayage pour n’importe quelle bande passante.
On peut également raisonner sur le temps de réponse du filtre. La réponse qui intervient est la
bande passante la plus faible si plusieurs filtrages interviennent. Pour une bande passante de 2Δf, on
peut évaluer ce temps à:

L'analyseur de spectre
4
τ=1/2Δf
Si T est le temps de balayage et E l’excursion de fréquence, la « vitesse » de balayage est:
v=E/T
Le temps que met l’analyseur à balayer une bande de fréquence équivalente à la largeur du
filtre est:
Δt=2Δf/(E/T)=2ΔfT/E
Ce temps doit rester grand devant le temps de réponse du filtre:
Δt>>τ
Soit, en reprenant les expressions à partir des grandeurs accessibles à l’utilisateur:
2ΔfT/E>>1/2Δf
En termes de temps de balayage:
T>>E/(2Δf)2
2.7. Modes de détection
Le signal qui sort du filtre de fréquence intermédiaire est variable dans le temps. Suivant sa
nature, on s'intéressera plus à sa valeur crête ou à sa valeur efficace.
La valeur crête peut être obtenue à l'aide d'un détecteur de crête classique comme celui de la
figure 4 où τd=R.C est grand devant la période de la FI.
Figure 4: Exemple de détecteur de crête
Pour obtenir la valeur efficace, on peut utiliser un dispositif de mesure dit "RMS" (root mean
square) thermique ou analogique. Dans les appareils modernes, on échantillonne le signal pour
calculer numériquement la valeur efficace. C'est le mode échantillonné.
Pour un spectre de raies, on doit utiliser un détecteur de crête et pour un spectre continu, on
préférera une détection échantillonnée.
2.8. Analyseur de spectre micro-onde
C'est un analyseur en bande de base précédé par un changement de fréquence supplémentaire
par mélangeur. La fréquence de l'oscillateur local en mode fondamental ou en mode harmonique
(mélangeur harmonique) est fixée de telle façon que la fréquence intermédiaire corresponde à la
bande de fréquence de l'analyseur de spectre. La fréquence intermédiaire utilisée est généralement
beaucoup plus faible que dans le cas précédent, de l'ordre de la centaine de MHz. Dans les
appareils anciens, on retrouve ainsi des bandes d'analyse de quelques GHz couvrant tout le spectre
micro-onde et sélectionnable manuellement. Les analyseurs de spectre modernes conservent le

L'analyseur de spectre
5
même principe, mais avec une commutation automatique permettant la couverture de tout le spectre
en un seul balayage. Pour les fréquences les plus élevées, un second mélangeur externe est ajouté,
l'analyseur de spectre fournissant éventuellement l'oscillateur local.
L'élimination des raies parasites (correspondant à d'autres mélanges que celui souhaité)
devient alors un véritable casse-tête. Aussi on utilise soit un système de reconnaissance automatique
des raies images ou correspondant à d'autres fréquences, soit un présélecteur qui ne laisse entrer
que les signaux contenus dans une bande centrée sur la fréquence étudiée. Il faut donc utiliser un
filtre passe bande accordable (filtre YIG) avec une commande en courant synchronisée avec le
balayage de fréquence de l'analyseur de spectre.
3. Précision de l’analyse spectrale
3.1 Limitations dues à l'appareil de mesure
L'analyse qui suit s'applique à une raie unique, infiniment fine, d'amplitude constante. Elle
permet de mettre en évidence les limitations liées à l'instrument de mesure.
3.1.1 Mesure de fréquence et de largeur de raie
La première source d'imprécision dépend directement du choix de la bande passante avant
détection. Elle portera sur la largeur du spectre mesurée. On obtient en fait la réponse spectrale de
ce filtre. C'est pourquoi la largeur mais aussi la raideur des flancs sont très importants.
La deuxième source d'erreur dépend de la stabilité de la source qui fournit l'oscillateur local
de l'analyseur. Ses fluctuations de fréquence seront directement transposées sur la mesure. Il est
illusoire d'espérer obtenir une résolution spectrale inférieure à la largeur spectrale de l'oscillateur
local. C'est pourquoi les appareils performants disposent d'une source synthétisée. Une mesure
relative de fréquence est toutefois possible si l'oscillateur local n'est pas synthétisé. On met à profit
la raie de mélange de l'oscillateur local avec lui même.
Pour mesurer les sources très stables, il peut être nécessaire de synchroniser la source et
l'oscillateur local de l'analyseur sur un quartz unique très stable. Dans ce cas la stabilité du quartz
n'intervient plus dans la mesure de la fréquence centrale (position et largeur de la raie) mais le bruit
de phase des deux sources n'est pas supprimé pour autant.
3.1.2. Mesure d'amplitudes des composantes spectrales
La troisième source d'erreur provient du mode de détection en fonction de la nature du signal.
La mesure d'un signal nécessite une détection crête pour être sûr de mesurer la puissance contenue
dans la bande d'analyse. Au contraire, lorsque c'est la valeur moyenne qui est significative (cas du
bruit), la détection doit se faire aléatoirement (mode échantillonnée).