Optique (Ex)

PCSI 2 Optique géométrique
2016 – 2017 1/10
OPTIQUE GEOMETRIQUE
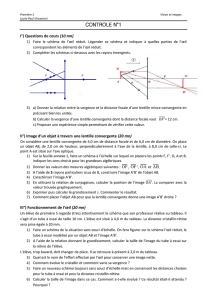
I Le microscope sera ici modélisé par une lentille mince convergente (L1) dite objectif, de centre optique O1 et de distance focale f'1 =
5 mm et une lentille mince convergente L2 appelée oculaire, de centre optique O2 et de distance focale f'2 = 2 cm. Les deux lentilles
sont coaxiales et leur distance O1O2 = l = 18,5 cm. L'objectif donne de l'objet AB une image A1B1 réelle agrandie, puis l'oculaire,
fonctionnant en loupe, donne de A1B1 une image finale A'B' virtuelle, agrandie, et renversée par rapport à AB. L'œil est situé au foyer
principal image F'2 de l'oculaire.
1) Déterminer la position de l'objet AB :
- lorsque l'observateur met au point l'image A'B' sur l'infini;
- lorsqu'il met au point cette image à 25 cm de l'œil.
En déduire la latitude de mise au point, c'est-à-dire la distance des deux positions précédentes de l'objet.
Montrer que ce résultat explique l'existence d'une vis micrométrique pour effectuer la mise au point.
2) Calculer le diamètre apparent α de l'objet AB, de 0,02 mm, vu à « l'œil nu » lorsqu'il est à 25 cm de cet œil, puis le diamètre
apparent α' de l'image A'B' lorsqu'elle est observée à l'infini.
Calculer le grossissement G =
€
α '
α
du microscope.
Réponse :
€
O1A
= -0,516 cm puis -0,515 cm; 1,55 µm; 400.
II Œil myope
Un œil myope a son punctum proximum à 12 cm et son punctum remotum à 1,2 m. Le centre optique de la lentille équivalente est à
15,2 mm de la rétine.
1) Entre quelles limites la distance focale de cet œil varie-t-elle ?
2) Déterminer la vergence de la lentille cornéenne qu'il faut lui adjoindre pour lui permettre une bonne vision de loin.
Indication : les vergences de lentilles accolées s’ajoutent.
3) Où le punctum proximum de l'œil corrigé est-il alors situé ?
Réponse : 1,35 cm et 1,5 cm; -0,877 δ; 13,41 cm.
III Macrophotographie
Un objectif photographique est constitué d'une lentille convergente L1 de centre O1, de distance focale image f'1 =
€
O1F'1
= 75 mm. La
position de la pellicule est définie par le point P tel que
€
O1F'1
≤
€
OP
≤
€
O1F'1
+ τ'; τ' = 4,25 mm est appelé le tirage de l'objectif.
1) On considère un objet
€
AB
= 1 cm situé à une distance
€
AO1
= 35 cm devant l'objectif dans un plan perpendiculaire à l'axe.
Peut-on photographier cet objet en ayant une image nette ?
2) On place devant l'objectif une lentille additionnelle L2 convergente de centre O
2, de vergence V2 = 3 δ à une distance
O1O2 = 5 cm constante.
a) Le tirage τ' de l'appareil étant inchangé, déterminer l'ensemble des points A de l'axe qui peuvent, après mise au point, être
photographiés en donnant une image nette.
b) On désire photographier l'objet défini à la question 1). La mise au point étant faite (on vérifiera qu'il est possible maintenant
d'avoir une image nette), calculer la grandeur
€
A'B'
de l'image portée sur la pellicule.
c) Faire un schéma du système qui, sans respecter l'échelle, respecte la position relative des différents éléments de l'appareil
photographique (positions des lentilles, foyers) et de l'objet. Tracer deux rayons issus du point B et en déduire l'image B' sur la
pellicule.
Réponse : non; 0 ≤
€
F
2A
≤ 66,06 mm; -2,52 mm.
IV Interposition d’une lentille
Une lentille convergente de distance focale f' = 20 cm est placée à 20 cm devant un écran. Un objet est placé à 30 cm en avant de la
lentille. Entre la lentille et l'écran, on place une deuxième lentille, la distance entre les deux lentilles étant 10 cm, de manière à obtenir
une image définitive nette sur l'écran.
Déterminer par le calcul la nature et la distance focale image de la lentille interposée.
Vérifier le résultat par une construction géométrique.
Réponse : f' = 12,5 cm.

PCSI 2 Optique géométrique
2016 – 2017 2/10
V Doubleur de focale
1) Un objectif d’appareil photographique peut être modélisé par une lentille convergente de focale f’1 = 50 mm. Le négatif se trouve
sur un écran plan fixe, perpendiculaire à l’axe optique de l’objectif. Pour la mise au point, on déplace l’objectif par rapport au
négatif. La distance d sur la figure 1 ci-dessous est donc variable mais ne peut excéder dmax = 100 mm.
Soit un objet haut de h = 2 m et distant de D = 50 m du négatif.
a) Montrer que la formule de conjugaison permet d’établir une relation entre d, D et f’1, relation qui se présente sous la forme
d’une équation du second degré en d.
b) Calculer alors d en tenant compte des contraintes pour l’objectif. Application numérique.
c) Déterminer la taille h’ de l’image sur le négatif. Application numérique.
2) On place maintenant entre l’objectif et le négatif un doubleur de focale assimilable à une lentille divergente f’2 = - 40 mm à une
distance d2 = 40 mm du négatif. La distance d’ entre l’objectif et le négatif peut maintenant atteindre d’max = 120 mm (figure 2).
a) Soient AB l’objet à photographier, A’B’ l’image de AB formée par l’objectif seul et A"B" l’image finale (celle de A’B’
formée par le doubleur de focale). A "B" étant sur le négatif, déterminer d1, distance entre A’B’ et le négatif. Vérifier à l’aide
d’un schéma. Application numérique.
b) Calculer le grandissement γ2 apporté par le doubleur de focale. Application numérique.
c) AB étant toujours à D du négatif, déterminer la distance d’ correspondante pour une mise au point nette. Application
numérique.
d) Calculer la nouvelle hauteur h" de l’image. Application numérique.
e) Déduire de tous ces résultats la signification du terme « doubleur de focale ».
Réponse : d2 – Dd + Df’1 = 0 ; d = 50,05 mm ; h’ = 2 mm ; d1 = 20 mm ; γ2 = 2 ; d’ = 69,95 mm ; h" = 4 mm.
VI Doublet
On étudie un doublet comportant deux lentilles L1 et L2, de centres O1 et O2 représenté sur la feuille 1.
Sur la gauche un rayon incident pénètre dans le système et émerge sur la partie droite, comme indiqué sur la figure.
Un carreau correspond à un centimètre.
1) Compléter sur la feuille 1 le trajet du rayon lumineux.
2) En déduire la nature de chacune des deux lentilles (convergente ou divergente ?).
3) Soient F1 et F’1 les foyers objet et image de la lentille L1, F2 et F’2 les foyers objet et image de la lentille L2.
Trouver graphiquement la position de ces foyers. Préciser les valeurs algébriques
€
O
1F'1
et
€
O2F'2
.
4) Qu’appellent-on foyer objet F, foyer image F’ d’un système optique ?
Trouver graphiquement la position des ces foyers. Préciser les valeurs algébriques
€
O
1F
et
€
O
1F'
. On choisira une couleur pour
chaque trajet réel des rayons lumineux.
5) Si
€
O
1F'1
= + 4 cm,
€
O2F'2
= - 2 cm et
€
O
1O2
= + 7 cm, déterminer par le calcul les valeurs algébriques
€
O
1F
et
€
O
1F'
.
d
Figure 1
F’1
Négatif
Objectif
d'
Figure 2
Doubleur
de focale
Négatif
Objectif
d2

PCSI 2 Optique géométrique
2016 – 2017 3/10

PCSI 2 Optique géométrique
2016 – 2017 4/10
Réponse : L1 convergente ; L2 divergente ;
€
O
1F'1
= + 3,8 cm ;
€
O2F'2
= - 2 cm ;
€
O
1F
= - 6,7 cm ;
€
O2F'
= - 1,2 cm ;
€
O
1F
= - 7,2 cm ;
€
O
1F'
= + 5,8 cm.
VII Lunette de Galilée
On désigne respectivement par
€
f
et
€
f'
les distances focales objet et image d’une lentille mince
€
L
de centre optique
€
O
et de foyers
principaux objet
€
F
et image
€
F'
. Un objet
€
AB
est disposé dans un plan de front de la lentille qui en donne une image
€
A'B'
.
1) Etablir la relation de conjugaison de Newton dans laquelle les positions sur l’axe optique
€
A
et
€
A'
des plans de front contenant
l’objet et l’image sont respectivement repérées par rapport aux foyers objet
€
F
et image
€
F'
.
2) Exprimer la relation de Newton donnant le grandissement transversal
€
Gt=A'B'
AB
de la lentille en fonction de la position
€
FA
de
l’objet par rapport au foyer objet
€
F
et de la distance focale image
€
f'
.
3) Une lunette de Galilée destinée à observer les objets terrestres est constituée d’un objectif convergent assimilable à une lentille
mince
€
L1
de centre optique
€
O
1
, de distance focale image
€
f'1=25cm
et d’un oculaire divergent que l’on peut également assimiler à
une lentille mince
€
L2
de centre optique
€
O2
et de distance focale image
€
f'2=−5cm
. Les axes optiques des deux lentilles sont
confondus et définissent l’axe optique de l’instrument.
Calculer numériquement la distance
€
e=O
1O2
entre les centres optiques des lentilles pour que le système soit afocal, c’est-à-dire
pour qu’un observateur dont l’œil est normal puisse voir en accommodant à l’infini l’image que donne la lunette d’un objet situé à
l’infini.
4) Un rayon lumineux entre dans l’instrument en faisant un angle
€
α
1
avec l’axe optique. Exprimer l’angle
€
α
2
que fait avec l’axe
optique, le rayon qui émerge de la lunette.
5) On définit le grossissement
€
G
d’un instrument par le rapport
€
G=
α
i
α
o
de l’angle
€
α
i
sous lequel un observateur voit un objet à
travers l’instrument sur l’angle
€
α
o
sous lequel il voit le même objet à l’œil nu. Calculer le grossissement
€
G
de la lunette dans le
cas de l’observation d’un objet à l’infini par un œil normal qui n’accommode pas.
6) La lunette étant toujours afocale, un objet de dimension
€
AB
est disposé dans le plan de front orthogonal à l’axe optique à une
distance finie
€
O
1A
de l’objectif de la lunette. L’objectif en donne une image intermédiaire
€
A'B'
reprise par l’oculaire qui en donne
une image définitive
€
A"B"
observable par un œil qui doit maintenant accommoder. Calculer dans ces conditions le grandissement
transversal de la lunette défini par le rapport
€
γ =A"B"
AB
.
Réponse :
€
FA.F'A'=−f'2
;
€
Gt=f'
FA
; e = 20 cm ; α2 = 5.α1 ; G = 5 ; γ = 0,2.
VIII Observation des anneaux de Saturne avec une lunette afocale.
Un astronome pointe sa lunette vers Saturne dans le ciel nocturne dégagé : on assimile cette planète à une source de lumière très
éloignée, notée A∞, et une portion de l’anneau le plus brillant à une autre source notée
B∞
(cf. figure 1 en annexe). Ces deux sources
sont séparées par une zone sombre. La lunette reçoit de chacune de ces deux sources des faisceaux de rayons parallèles, l’axe de la
lunette étant parallèle à ceux venant de A∞. Le rayon de l’anneau est de l’ordre de RA = 108 m, la distance entre la Terre et Saturne est
de l’ordre de D = 1,5.1012 m. On note α l’angle entre les deux directions. La lunette forme un système afocal, c’est-à-dire qu’il ne
possède pas de foyer : deux rayons incidents parallèles émergent parallèlement du système optique. Elle est constituée de deux lentilles
minces : la première, l’objectif, a pour centre O1 et pour vergence V1 = 1/f’1 = +1,0 δ ; la seconde, l’oculaire, a pour centre O2 et pour
vergence V2 = 1/f’2 = -5,0 δ ; elles sont écartées de
€
O
1O2= +0,80m
. La figure 1, complétée, sera rendue avec la copie : l’échelle sur
l’axe est 1/10 et l’angle α est volontairement exagéré. Les conditions de Gauss sont supposées vérifiées.
1) Calculer numériquement l’angle α.
2) Construire l’image
€
A
1B 1
de
€
A∞B∞
par l’objectif. Est-ce une image réelle ou virtuelle ? Sera-t-elle considérée comme un objet
réel ou virtuel pour l’oculaire ?
3) Tracer des rayons émergents issus de A1 et B1 après traversée de l’oculaire. Expliquer pourquoi cette lunette est bien afocale.
4) On note α’ l’angle entre la direction des faisceaux de rayons émergents issus de A∞ et celle des rayons émergents issus de B∞. On
appelle grossissement le rapport G = α’/α. Exprimer la valeur absolue de G en fonction de f’1 et f’2 et la calculer numériquement.
5) L’œil, sans instrument d’optique, ne peut distinguer deux rayons que si l’angle qui les sépare est supérieur ou égal à αo = 1,0.10-4
rad (c’est le pouvoir séparateur de l’œil). Vérifier que l’utilisation de la lunette est indispensable pour distinguer les anneaux de
Saturne.
6) Une caméra numérique remplace l’œil derrière l’oculaire : elle est constituée par une lentille convergente de vergence V3 = + 50
δ (remplaçant le cristallin) et une plaque tapissée de cellules photosensibles en nid d’abeille distantes de 1 µm (remplaçant les

PCSI 2 Optique géométrique
2016 – 2017 5/10
cellules de la rétine) placée dans le plan focal de la lentille. Sur la figure 2 en annexe, on a noirci les cellules recevant de la lumière
venant de la planète Saturne elle-même (où il apparaît qu’elle n’est pas réellement ponctuelle car son image occupe plusieurs
pixels) ; noircir les cellules qui recevront de la lumière venant de l’anneau (on suppose qu’il est vu de face et de faible largeur). En
déduire pourquoi on peut effectivement reconnaître la forme d’un anneau. La figure 2, complétée, sera rendue avec la copie.
ANNEXE (à rendre avec la copie)
Réponse : α = 0,67.10-4 rad ;
€
G=5
.
IX Détection automatique de la pluie
De nombreux dispositifs d’aide à la conduite sont apparus ces dernières années, comme par exemple la détection automatique de pluie
qui commande la mise en route des essuie-glaces.
Disposé à l’intérieur du véhicule, une diode électroluminescente (DEL) projette un faisceau lumineux sur le pare-brise. Un capteur
reçoit et mesure en permanence la lumière réfléchie.
Plus il y a d’eau sur la vitre, moindre est la réflexion. Le capteur de pluie pilote ainsi l’essuie-glace en fonction de la quantité d’eau
détectée et sélectionne automatiquement la vitesse d’essuyage la plus efficace.
Figure 2
(Les 19 pixels de la tache formée par Saturne ont été grisés)