Feuille d`exercices : Condensateur Exercice n°2 : Exercice n°3

Lycée Paul Langevin Première génie électronique M. GOLAIN
Feuille d’exercices : Condensateur
Exercice n°1 : Cocher et justifier sur votre feuille la bonne réponse pour les questions ci-
dessous.
1) L'espace situé entre les armatures d'un condensateur est :
 conducteur  isolant  semi-conducteur
2) La valeur de la charge q accumulée sur l'armature B
du condensateur ci-contre est :
 10 µC  - 10 µC  0 C
3) Deux condensateurs C1 = 47µF et C2 = 100 µF (initialement déchargés) sont associés
en série et l'ensemble est soumis à une tension. On a alors a tout instant pour les tensions:
 u
C1
> u
C2
 u
C1
< u
C2
 u
C1
= u
C2
4) Un condensateur soumis à la tension U = 10V présente,
sur une plaque, la charge q = 10
-5
C (schéma ci-contre):
Sa capacité est de :
 100 kF  100 µF  1 µF
5) Un condensateur C = 4700 µF a été chargé avec un courant constant I = 0,5 mA
pendant t = 1 min. La tension à ses bornes est :
 30 mV  ≈ 6,38 V  141 µV
6) L'énergie emmagasinée dans un condensateur de 330 nF ayant une tension de 10 V est
de :
 16,5 µJ  1,65 µJ  33 µJ
7) On charge un condensateur C = 470 µF avec un courant constant I = 0,1 mA.
Le condensateur atteindra une tension u = 5 V au bout d'un temps de :
 6 min 48 s  ≈ 2 jours  23,5 s
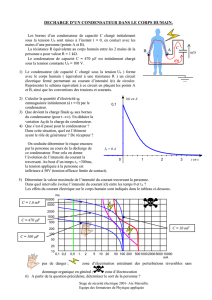
Exercice n°2 :
Un condensateur de capacité C est
traversé par un courant constant
I = 0,5mA.
La tension u(t) aux bornes du
condensateur est représenté ci-
contre :
Question : déterminer la valeur de
la capacité C.
Exercice n°3 :
Un condensateur de capacité
C = 470 pF est traversé par un
courant constant I.
La tension u(t) aux bornes du
condensateur est représentée ci-
contre :
Question : déterminer la valeur de
l'intensité du courant I.
Exercice n°4 :
On a utilisé un condensateur de capacité C = 2200 µF pour emmagasiner une énergie
électrique W = 58,19 J.
Question : déterminer la valeur de la tension U aux bornes du condensateur.
Exercice n°5 :
Le montage représenté ci-dessous représente la charge d'un condensateur C = 10µF à
l'aide d'une tension E = 5 V constante et à travers une résistance R = 2,2 kΩ.
L'interrupteur K est ouvert à partir de l'instant t = 0.
1) Quelle est la valeur de la tension u
C
avant l'ouverture de l'interrupteur K.
2) Par quel dipôle (K ou C ?) passe le courant i avant l'ouverture de l'interrupteur K.
3) Calculer la valeur du temps t
1
au bout duquel la tension u
C
atteint » 3,15 V.
4) On réalise un autre essai avec R réglable et on désire que la tension u
C
atteigne la
valeur 4,75 V au bout d'un temps t
2
= 10 µs. Calculer alors la valeur de la résistance R.
Exercice n°6 :
On prend un condensateur de capacité C
1
= 470 mF et chargé avec la tension U
1
= 24 V.
1) Calculer la valeur de l'énergie W
1
emmagasinée par C
1
.
On prend un deuxième condensateur de capacité C2 = 1000 mF déchargé (U
2
= 0 V).
2) Quelle est la valeur de l'énergie W
2
emmagasinée par C
2
.
On branche maintenant les deux condensateurs C
1
et C
2
en parallèle.
3) Déterminer la valeur de la tension U aux bornes des deux condensateurs.
4) Calculer la valeur de l'énergie W
12
emmagasinée par l'ensemble C
1
// C
2
.
Comparer W
12
avec W
1
+ W
2
et donner une explication au résultat.

Lycée Paul Langevin Première génie électronique M. GOLAIN
Exercice n°7 :
On désire réaliser une fonction de type temporisation dans laquelle une lampe devra rester
allumée 3 minutes après appui puis relâchement d'un bouton poussoir (minuterie
d'escalier).
Le montage est représenté ci-dessous :
Le fonctionnement du montage est le suivant :
- au repos, le bouton poussoir est "ouvert" ;
- le courant i
e
en entrée de la porte logique (porte CMOS) est négligeable ;
- si u
C
< 2,5 V (V
CC
/ 2) alors la lampe s'allume (sortie porte logique
"NAND"= 5 V);
- si u
C
> 2,5 V alors la lampe s'éteint (sortie porte logique "NAND"= 0 V).
1) Bouton poussoir "ouvert" (repos) :
Donner la valeur du courant i ainsi que la valeur de la tension u
C
(système au repos depuis
longtemps). En déduire l'état de la lampe (éteinte ou allumée).
2) Bouton poussoir maintenu appuyé :
a) Donner la valeur du courant i (en fonction de E et R) ainsi que la valeur de la
tension u
C
(poussoir maintenu appuyé). En déduire l'état de la lampe (éteinte ou
allumée).
b) Quels sont les composants qui seront traversés par le courant i.
3) Bouton poussoir relâché à partir de l'instant t = 0 :
a) Dessiner rapidement l'allure de la tension u
C
(t) en représentant l'instant
t
1
= 3min où la lampe va s'éteindre.
b) Déterminer la valeur de la résistance R qui va permettre d'avoir t
1
= 3min.