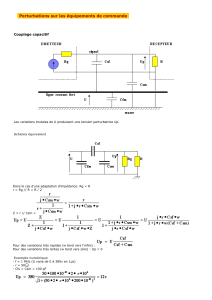
Couplage uide-structure partitionné avec une chaîne de calculs

er

•Ωf
•Ωs
•Γ
•n
•TN
•d
•u˚ d
•λ
Sf
Sf(df) = λf
S−1
s
S−1
s(λs) = ds
ds=df=dΓsur Γ×[0; T]
λs+λf= 0 sur Γ×[0; T]
Sf(dΓ) + Ss(dΓ) = 0 sur Γ×[0; T]
S−1
s(−Sf(dΓ)) = dΓsur Γ×[0; T]
dNdΓλNλΓTN
G
G=S−1
s◦ −Sf

TNTN+1
dN+1 =S−1
s(−Sf(dN))
P
dN+1 =S−1
s−SfdP N+1
Tinit Tfin N0
∆t Tinit
T←Tinit
N←N0
T < Tfin
dP
N+1 =P(dN,˚
dN,dN−1, ...)
λN+1 =Sf(dP
N+1)
dN+1 =S−1
s(λN+1)
N←N+ 1 T←T+ ∆t
P(dN,˚ dN,˚ dN−1) = P(dN,uN,uN−1) = dN+α0∆tuN+α1∆t(uN−uN−1)
α0= 1 α1= 0.5
dP
N+1 =dN+∆t
2(3uN−uN−1)
α0= 0 α1= 0 α0= 1 α1= 0
dN+1
dP
N+1
TNTN+1
λ∗
N=λN+λN+1
2