Proposition d`examen d`optique en PHY 111 et PHY 112

Licence 1 – UE PHY112 – Examen d’optique
1ère session – novembre 2008 – corrigé et barème
Aucun document n’est autorisé – calculatrices acceptées
Le sujet comporte 4 pages dont 1 document-réponse à rendre avec la copie
La présentation et la clarté des explications sont évaluées
Prisme : / 05 pts
Tracés de rayons : / 09 pts
Etude de l’œil : / 14 pts
Présentation de la copie et clarté des explications : / 02 pts
Total (à ramener sur 20) : / 30 pts
Si possible, les ½ points seront évités, le barème étant assez détaillé.
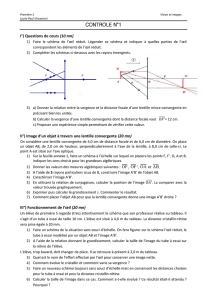
1 Réalisation d’un périscope à réflexion totale (/ 5 points)
Un périscope est un système optique assez simple, basé sur deux miroirs. Bien souvent, les
miroirs métalliques sont remplacés par des prismes dits « à réflexion totale ».
C
B
A
Prisme
Miroir
Les prismes utilisés sont rectangles et isocèles (les angles valent 90°, 45° et 45°). Ils sont
taillés dans un matériau transparent d’indice n.
1. Définir par un schéma l’angle d’incidence au point B. Quelle est sa valeur ?
1 point
(valeur) L’angle d’incidence est défini par rapport à la normale à l’interface ; il vaut 45°.
A B
C
1 point
(schéma)

2. Le périscope étant plongé dans l’air, à quelle condition sur l’indice n du prisme y-
a-t’il réflexion totale ?
La condition de réflexion totale est 1 sin air
n
in
−⎛⎞
>⎜⎟
⎝⎠
1 point ,
donc la condition sur l’indice du prisme est
1 point 121,41
sin( )
ni
>=≈.
On utilise désormais ce dispositif dans un périscope à eau (l’ensemble du tube périscopique
est immergé dans l’eau, d’indice 1,33).
3. Donner une valeur de l’indice n du prisme qui permette d’obtenir la réflexion
totale et donc l’effet périscopique dans cette nouvelle configuration.
La réflexion totale a alors lieu si 1 sin eau
n
in
−⎛⎞
>⎜⎟
⎝⎠
, donc si 1,875
sin( )
eau
n
ni >≈
1,9n=
.
est par exemple une valeur qui convient.
1 point
2 Tracés de rayons (/ 9 points)
Pour chacun des 3 cas proposés, compléter le document-réponse fourni en fin d’énoncé :
1 point « nature »
(cases) pour chaque cas
1 point « image »
pour chaque cas
1 point « foyers »
pour chaque cas - placer sur le schéma les foyers (objet et image) des lentilles ou du
système ;
- trouver la position de l’image A’B’ de l’objet AB ;
- préciser la nature (réelle ou virtuelle, droite ou inversée, agrandie ou
rétrécie) des images obtenues.
a) Une lentille convergente avec une distance focale de 4 cm.
b) une lentille divergente avec une distance focale image de – 3 cm.
c) une lentille convergente avec une distance focale image de 4 cm suivie d’une lentille
divergente avec une distance focale image de – 1 cm, séparées de 4 cm.
Tous les résultats seront notés sur le document-réponse (les réponses aussi !).

3 Etude de l’œil (/ 14 points)
A- Œil emmétrope (sans défaut)
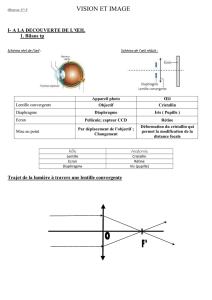
L’œil humain peut être décrit simplement par une lentille mince convergente L1 de focale
image f1’ et par un écran E séparés d’une distance fixe d = 20mm. La lentille mince décrit à la
fois la cornée et le cristallin. La particularité de cette lentille est qu’elle a une distance focale
image variable : c’est l’accommodation qui permet d’observer des objets situés à différentes
distances. Lorsque l’œil est au repos (pas d’accommodation), la focale image f1’ d’un œil
emmétrope est égale à +20mm.
L’écran matérialise la rétine.
Votre œil observe un oiseau de 25cm de haut situé à une distance de 50m.
3.1 Votre oeil doit-il accommoder pour observer l’oiseau de façon nette ?
Pour répondre à cette question de façon rigoureuse, on doit déterminer la position
où se forme l’image de l’oiseau. On utilise pour cela la relation de conjugaison
d’une lentille mince :
''
'
2
11 1
V , , ' '
'
50
' 2 10 20
ou p SA p S A f SF
pp f
pm
pmmm
−
−== = = =
=−
≈⋅ =
Une autre façon de répondre, tout aussi valable, est que compte tenu des ordres de
grandeurs de f’=20mm et de p=-50m, l’objet peut être considéré comme étant à
l’infini…
On a donc une image qui se forme dans le plan focale image.
L’œil n’a pas besoin d’accommoder.
3.2 Quelle est la taille de l’oiseau sur la rétine ? L’image est-elle droite ou renversée ?
Pour déterminer la taille de l’image sur la rétine on doit calculer le grandissement
du système optique :
24
424
' or pour notre situation ' '
'210 410
50
' ' 4 10 25 10 10 0,1 100
ppf
p
f
p
AB AB m mm µm
γ
γ
γ
−−
−−−
==
⋅
== =−⋅
−
=⋅ =−⋅ ⋅ ⋅ =− =− =−
L’image de l’oiseau sur la rétine fait 0,1mm.
Le grandissement est négatif donc l’image est renversée par rapport à l’objet.
1 point
1 point
1 point

Vous voulez désormais observer un crayon posé devant vous, à 40cm de votre œil.
3.3 Dans le cas où votre œil reste au repos, où se forme l’image du crayon ?
Commentez le résultat obtenu...
Pour répondre à cette question, on doit déterminer la position où se forme l’image
du crayon. On utilise pour cela la relation de conjugaison d’une lentille mince :
''
'
22
2
11 1
V , , ' '
'
40 10 et ' 2 10 20
'
' 2,1 10 21
'
ou p SA p S A f SF
pp f
pmfmmm
pf
pmmm
pf
−−
−
−== = = =
=− ⋅ = ⋅ =
==⋅=
+
On a donc une image qui se forme environ 1 mm derrière la rétine. L’image est
floue.
3.4 Quelle doit être la nouvelle valeur de la distance focale de la lentille convergente L1
pour que l’image soit nette sur la rétine ?
Pour répondre à cette question, on doit déterminer la distance focale qui permet de
former sur la rétine l’image d’un objet situé à 40cm. On utilise pour cela la
relation de conjugaison d’une lentille mince :
''
'
22
2
11 1
V , , ' '
'
40 10 et ' 2 10 20
'
' 1,9 10 19
'
ou p SA p S A f SF
pp f
pmpmmm
pp
fmmm
pp
−−
−
−== = = =
=− ⋅ = ⋅ =
==⋅=
−
La valeur de la distance focale pour laquelle on aura une image nette sur la rétine
est de 19mm.
3.5 L’œil est-il plus convergent ou moins convergent que s’il n’accommode pas?
La nouvelle valeur de la distance focale de la lentille mince modélisant l’œil est
plus courte, on a donc une lentille plus convergente que celle de l’œil au repos.
1 point
1 point
1 point
Le pouvoir d’accommodation de l’œil permet de diminuer la distance focale f1’ de la lentille
convergente L1 de 1,5mm par rapport à sa valeur au repos.
3.6 Déterminer alors la distance minimale, notée DPP, pour laquelle l’œil peut voir net.
L’objet situé à cette distance est alors au punctum proximum.
Quel est le grandissement du système optique « œil » dans cette configuration ?
Pour répondre à cette question, on se place au maximum d’accommodation de
l’œil, c'est-à-dire pour une distance focale image de 20mm – 1,5mm = 18,5mm et
on détermine la distance objet-lentille pour laquelle on a une image nette sur la
rétine. On utilise pour cela la relation de conjugaison d’une lentille mince :

''
'
22
2
11 1
V , , ' '
'
' 1,85 10 18,5 et ' 2 10 20
'' 24,7 10 24,7
''
ou p SA p S A f SF
pp f
f
m mmm p m mm
fp
pmcm
fp
−−
−
−== = = =
=⋅ = =⋅ =
⋅
==−⋅=−
−
On trouve donc que Dpp est égale à 24,7cm.
Le grandissement du système optique est alors égale à :
22
2
'210 8,1 10 0.081
24,7 10
p
p
γ
−−
−
⋅
== =−⋅ =−
−⋅ .
3.7 Sachant que la distance entre deux cellules rétiniennes est de 2.5 µm, en déduire la
dimension du plus petit détail que peut distinguer l’œil sur un objet situé au
punctum proximum.
Le plus petit détail correspond à un objet de dimensions telles que l’on aura une
image de dimensions supérieures à 2,5µm.
On utilise alors le grandissement au punctum proximum :
6
'' 0.081
''2,5
'' 2,510 30,9
0.081
AB
AB
AB µm
AB
AB µm
γ
γ
−
==−
=
⋅
== =−
−
Donc la dimension du plus petit détail que l’œil puisse distinguer est d’environ
31µm.
1 point
1 point
1 point
B- Œil myope
L’œil myope est un œil qui est trop convergent lorsqu’il est au repos, c'est-à-dire que la
focale image f1’ de la lentille L1 n’est plus égale à 20mm. On prendra pour notre œil myope
au repos une lentille L1 avec une distance focale image f1’ égale à +18mm. Cet œil observe
toujours un oiseau de 25cm de haut situé à une distance de 50m.
3.8 Déterminer la position où se forme l’image de l’oiseau lorsque l’œil myope est au
repos, et commentez la valeur obtenue.
Pour répondre à cette question, on peut déterminer la position où se forme l’image
de l’oiseau. On utilise pour cela la relation de conjugaison d’une lentille mince :
''
'
2
2
11 1
V , , ' '
'
40 et ' 1 80 20
'
' 1,8 10 18
'
ou p SA p S A f SF
pp f
pmf mmm
pf
pmmm
pf
−
−
−== = = =
=− = ⋅ =
==⋅=
+
Une autre façon de répondre, tout aussi valable, est que compte tenu des ordres de
grandeurs de f’=18mm et de p=-50m, l’objet peut être considéré comme étant à
l’infini…