I LES FLUIDES 1. Introduction

Université Paul Sabatier - FSI L2 Mécanique / Mathématiques
I
LES FLUIDES
1. Introduction
Le but de la mécanique en général est d’étudier le mouvement (y compris l’immobilité) d’un
« système », et de relier ce mouvement à ses causes.
Nous nous intéresserons ici aux fluides, ou milieux fluides, très présents dans la nature et les
systèmes industriels, qu’il faut tout d’abord savoir définir et caractériser.
La mécanique des fluides a pour objet d’une part l’étude des comportements statique et
dynamique des fluides, et d’autre part l’étude des interactions entre fluides et solides.
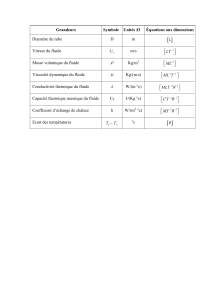
a) Grandeurs physiques
Les grandeurs physiques que nous rencontrerons sont le résultat d’une mesure ou d’un calcul.
Elles sont données sous forme d’un produit constitué d’une valeur numérique et d’une unité :
uniténumériquevaleurphysiqueGrandeur
×
=
Exemples : , …
KT 273=mbarsPatm 1013=
Un résultat numérique sans unité n’a aucun sens physique.
Les unités pour les grandeurs physiques sont fixées par Système International d’unités (S.I.).
Ce système est fondé sur 7 grandeurs fondamentales qui définissent les unités de base (cf L1):
Dimension Longueur Masse Durée Intensité
de courant Température Quantité de matière
Intensité
photométrique
Unité m kg s A K mol Cd
b) Dimensions
L’équation aux dimensions d’une grandeur physique est son expression en fonction des
grandeurs fondamentales. Les différents membres d’une formule ou d’une équation physique
doivent toujours satisfaire à ces équations aux dimensions, c'est-à-dire vérifier la même
relation entre grandeurs fondamentales.
Mécanique des fluides Manuel Marcoux I - 1

Université Paul Sabatier - FSI L2 Mécanique / Mathématiques
Exemple : 00
2
21)( xtvtatx ++= (Chute libre) →
[
]
2
.− =sma et
[]
1
0.−
=smv
Lors de calculs, il est utile de vérifier la dimension du résultat.
Pour trouver la dimension (ou l’unité) d’une grandeur dérivée, il faut retrouver une formule
simple donnant sa définition en fonction des grandeurs fondamentales (ou d’une combinaison
des grandeurs fondamentales)
Exemple : la force F, en Newtons :
∑
=amFPFD
r
r
: →
[
]
2
.. − =smkgF
Remarque : Lorsque toutes les dimensions disparaissent après simplification, le résultat
obtenu est dit sans dimension, son expression se réduit alors à une valeur chiffrée.
Jamais le cas cette année
2. Notions générales
a) Etats de la matière
On distingue naturellement (par le sens du toucher) trois états de la matière, les états :
solide, liquide et gazeux.
Origine Physique : Déformation
 L’effort à fournir pour modifier la forme d’un solide est beaucoup plus important que
pour un gaz ou un liquide (dans un récipient souple).
 Dans la déformation d’un gaz ou d’un liquide, les molécules ne gardent pas leur place
attitrée, alors que pour un solide elles conservent les mêmes voisins.
⇒ Ces états sont caractérisés par la mobilité des éléments qui constituent le milieu considéré,
il faut chercher la différence de comportement au niveau atomique (liaisons interatomiques).
De façon général, les atomes (ou molécules) d’un corps à une certaine température possèdent
une agitation thermique (plus ou moins forte pour une température plus ou moins élevée).
L’intensité des forces d’attraction interatomiques ou intermoléculaires tendent à maintenir une
cohésion d’ensemble, mais l’agitation thermique est une force antagoniste qui a pour effet
d’éloigner les atomes les uns des autres, ce qui s’oppose à la rigidité du milieu.
Mécanique des fluides Manuel Marcoux I - 2

Université Paul Sabatier - FSI L2 Mécanique / Mathématiques
On peut alors distinguer :
L’état solide : L’effet de l’agitation thermique est négligeable devant les forces de liaison
interatomiques. Les molécules vibrent autour d’une position moyenne, mais sans se déplacer
les unes par rapport aux autres
(densité de matière élevée, organisation forte, compacité) → ordre à longue distance
Etat gazeux : les atomes n’ont quasiment aucune interaction les uns avec les autres, et
l’agitation thermique introduit un désordre total. Cet état est souvent idéalisé par un « nuage »
de molécules n’ayant aucun interaction entres elles en dehors des chocs, supposés
parfaitement élastiques et occasionnés seulement par l’intersection de leur trajectoires
(nombre de chocs de l’ordre du milliard par seconde) → aucun ordre, atomes indépendants
Etat liquide : Etat intermédiaire entre solide et gaz. L’agitation est suffisante pour rompre les
liaisons fortes du solide, les molécules se déplacent librement, mais les forces d’attraction
intermoléculaires sont suffisamment fortes pour les retenir à faible distance.
→ ordre à courte portée, l’état est désordonné, mais le volume est défini
Les liquides vont donc occuper un volume bien déterminé, limité par une surface bien définie
(qui variera peu sous l’effet de la pression ou de la température).
Les liquides, dépourvus de rigidité, n’ont pas une forme qui leur est propre et n’opposent pas
de forte résistance à la déformation (même caractère « fluide » que celui observé chez les gaz)
C’est ce que nous allons principalement traiter dans ce module.
La faible résistance à la déformation est ce que l’on appelle viscosité, elle ser négligée dans
un premier temps (fluide parfait)
Les liquides et les gaz forment les fluides : à l’échelle macroscopique (observation à l’œil
nu), ils présentent un aspect continu, aisément déformable, sans forme propre, et pouvant
s’écouler (d’où le nom de fluide)
b) Changements d’état
Un corps pur peut passer d’un état à un autre (changement de phase) en subissant une
transformation bien déterminée.
Mécanique des fluides Manuel Marcoux I - 3

Université Paul Sabatier - FSI L2 Mécanique / Mathématiques
Diagramme de phases
L’état d’un corps pur en règle générale dépend de trois variables : pression (P), volume (V) et
température (T).
Dans des conditions données de pression et de température un corps pur n’est stable que dans
une seule phase (généralement) sauf :
- au point triple où les 3 phases coexistent à une température et à une pression données,
- pour un couple (pression, température) correspondant à une transition de phase.
- au dessus du point critique, limite de la courbe de vaporisation au dessus de la quelle le
liquide ne peut se vaporiser et le gaz ne peut se liquéfier.
Dans ces conditions : Gaz ≈ Liquide (continuité de l’état liquide)
Exemple : Cas de l’eau
Point glace : , , Point vapeur : 1.013
G
P bar=0
G
T=°C1.013
V
Pbar
=
, TC 100
V=°
CPoint triple : , , Point critique : 0.0061
T
P bar=0.010
T
T=° 221.2
C
Pbar
=
, TC 374.1
C=°
Pour plus de détails, voir le module de thermodynamique. Dans cette introduction à la
mécanique des fluides, nous ne traiterons essentiellement que de liquides.
c) Définition des fluides en mécanique
En mécanique, on appelle fluide un milieu considéré comme continu à l’échelle
macroscopique (pas d’étude au niveau des atomes), sans rigidité, pouvant subir de grandes
déformations non élastiques sous l’action de forces qui peuvent être très faibles.
Mécanique des fluides Manuel Marcoux I - 4

Université Paul Sabatier - FSI L2 Mécanique / Mathématiques
Il n‘a pas de forme propre (il prend la forme du récipient qui le contient) et il présente la
propriété de pouvoir s’écouler.
La plupart des liquides, gaz et vapeurs répondent sans ambiguïté à cette définition
Remarques
- Cette définition du fluide comporte cependant des points faibles qui rendent certaines
substance difficiles à classer : pâtes, purées, gels, pommades, graisse, boues …
Ces substances ont généralement des comportements particuliers dont l’étude relève d’une
branche spécifique de la mécanique des fluides appelée rhéologie (fluides non newtoniens).
-En mécanique des fluides, on peut aussi différencier les solides des fluides en utilisant les
échelles de temps. Ainsi, sur des temps courts (s, min, h), le manteau terrestre est aperçu
comme immobile et est considéré comme un solide, alors que sur des temps longs (annees),
un mouvement de convection est observable et le > manteau est considéré comme un fluide
- Par ailleurs, un grand nombre de solides finement divisés présentent aussi la possibilité de
pouvoir s’écouler (sable sec, sucre, sel, graines poudres …). Entraînés dans les courants
liquides (suspensions), ils évoluent alors comme des fluides, et sont étudiés comme milieux
fluidisés ou dispersés.
On rencontre l’appellation « fluide parfait » désignant un fluide imaginaire totalement
dépourvu de frottements internes (pas de viscosité), ils n’offrent donc aucune résistance à la
déformation.
Cette hypothèse facilite l'étude théorique des écoulements, car les résultats obtenus sont
applicables en première approximation aux fluides réels dans des conditions ou les
frottements internes sont très faibles (gaz s’écoulant à faible vitesse …).
→ cf. chapitre sur les fluides parfaits
Au repos, tous les fluides réels peuvent être assimilés à des fluides parfaits.
→ cf chapitre suivant sur l’hydrostatique
d) Description d’un fluide
Comme on l’a vu précédemment, de manière générale, l’état d’un fluide peut être défini à
partir des trois variables : pression P, volume V (ou mass volumique
ρ
) et température T.
Dans le cas de fluides en écoulement, il convient d’ajouter la vitesse v et le débit q
Mécanique des fluides Manuel Marcoux I - 5