Électromagnétisme : Devoir Maison n˚1 — LP 205 — 1

Électromagnétisme : Devoir Maison n˚1
— LP 205 —
Électromagnétisme dans l’atmosphère
Brahim Lamine &Nicolas Treps
23 mars 2006
Ce problème est constitué de deux parties indépendantes. Les questions difficiles, qui de-
mandent une certaine autonomie, sont marquées d’une étoile.
1 Électromagnétisme dans l’atmosphère
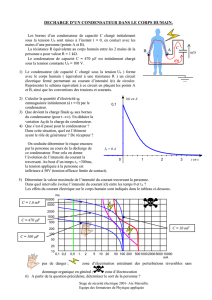
L’état électrique de l’atmosphère, par beau temps, peut être modélisé comme suit : le sol et
l’ionosphère, qui est une couche parfaitement conductrice située à 15 km du sol, forment deux
sphères conductrices imbriquées l’une dans l’autre.
1. On appelle R1et R2les rayons respectifs de la terre et de l’ionosphère. On suppose que la
terre porte une charge Q1.
a) En utilisant le théorème de Gauss, exprimer le champ
électrique E(r)qui règne entre les deux sphères en
fonction de la distance rau centre de la terre. On dé-
taillera les symétries et invariants utilisés pour déduire
la direction et les variables dont dépend le champ élec-
trique.
b) À l’aide de la relation E(r) = −dV(r)
dr, déterminer le
potentiel V(r)entre les sphères.
c) En utilisant le théorème de Gauss avec une surface de
Gauss qui est une sphère de rayon compris entre R2
et R3et en utilisant le fait que la ionosphère est un
conducteur parfait, montrer que la charge portée par
la surface intérieure de la ionosphère est opposée à la
charge de la terre.
R1
R2
Terre
Air
Ionosphère
R3
Un peu de cours : Ce système de deux sphères imbriquées forme ce que l’on ap-
pelle un condensateur car l’ensemble des lignes de champ issues de la sphère terrestre
aboutissent sur la ionosphère (et réciproquement). On montrera dans le cours que,
de manière générale, quand deux conducteurs en regard ont leur lignes de champ
qui vérifient cette propriété, ils portent sur leur surfaces en regard des charges oppo-
sées. Cette charge s’appelle la charge du condensateur. On définit alors la capacité
d’un condensateur de façon équivalente à celle d’un conducteur : c’est le rapport
entre la charge du condensateur et la différence de potentiel entre les deux armatures
C=Q1
V1−V2. L’énergie d’un condensateur a alors la même expression que celle d’un
conducteur.
d) En déduire l’expression de la capacité Cdu condensateur terrestre en fonction de R1
et R2.
Application numérique : R1= 6400 km et ε0= 8,8×10−12 S.I.
1

Licence de physique LP205 Année 2005-2006
e) Diverses mesures montrent que le champ électrique ~ Eau niveau du sol est de l’ordre
de 150 V/m et que la Terre est chargée négativement. Quelle est la charge totale de
la Terre et la différence de potentiel entre le sol et la haute atmosphère ?
f) En déduire l’énergie stockée sous forme électrostatique par l’atmosphère.
2. En fait, l’atmosphère située entre la terre et l’ionosphère est légèrement conductrice en
raison de la présence d’ions des deux signes capables de se déplacer sous l’action du champ
électrique régnant dans l’atmosphère. On considère en particulier les « petits ions » de
charge positive ou négative e= 1,6×10−19 C. La mobilité des ions positifs est µ+=
1,4×10−1m2s−1V−1et celle des ions négatifs est µ−= 1,9×10−4m2s−1V−1. On rappelle
que par définition un ion de mobilité µplacé dans un champ électrique ~ Eacquiert une
vitesse ~v =µ~ E.
a) On cherche tout d’abord à modéliser la mobilité des ions en supposant que la conduc-
tivité finie de l’atmosphère provient d’une force de frottement visqueux exercée par
l’air sur les ions. Écrire le principe fondamental de la dynamique pour une particule
de charge q, de masse m, soumise à un champ électrique ~ Econstant et à une force
de frottement de type visqueux ~ F=−α~v.
b) Résoudre l’équation précédente pour trouver ~v(t). Quelle est l’expression de la vitesse
pour t→+∞?
c) En déduire l’expression de la mobilité de cette particule.
d)* Montrer que le courant global Iair-Terre pour l’ensemble du globe s’écrit :
I=neQ
ε0
(µ+−µ−)(1)
où nest la concentration en ions de chaque signe.
Application numérique : calculer I. On prendra n'500 cm−3.
e)* Quel est le temps au bout duquel la charge terrestre serait réduite au centième de sa
valeur initiale en admettant que le courant dû au phénomène précédent soit le seul
en cause ?
3. Le champ électrique terrestre existant depuis un temps très supérieur à celui déterminé
dans la question précédente, il existe un mécanisme capable de recharger le condensateur
terrestre. L’hypothèse généralement admise est qu’il s’agit des orages. Au cours d’un orage,
des éclairs jaillissent entre le sol et les nuages. Un éclair peut être assimilé à un courant
rectiligne de diamètre D= 25 cm transportant un courant d’intensité I= 105A. On donne
µ0= 4π×10−7S.I.
a) Calculer le champ magnétique créé par l’éclair en fonction de la distance dà l’axe de
l’éclair. On admettra pour fixer les idées que l’éclair est vertical.
b) Une aiguille de boussole est un aimant permanent. Elle peut se désaimanter lorsqu’elle
est placée dans un champ supérieur à 2,4×10−3T. Jusqu’à quelle distance du point
d’impact de l’éclair la boussole risque t-elle d’être désaimantée ?
Devoir maison numéro 1 2 B Lamine, N Treps

Licence de physique LP205 Année 2005-2006
2 Exercices d’entraînement
2.1 Champ électrique
1. Calculer le champ électrique aux points M
qui figurent sur les schémas ci-contre.
Le schéma de gauche représente deux plans infi-
nis chargés respectivement σ1et σ2. Le schéma de
droite représente un disque uniformément chargé
en surface σ.
a
s1
s2
x
y
z
z
Ms
OM
2. Calculer le champ électrique créé par un fil infini dont la
charge par unité de longueur est noté λ, en un point M
situé à une distance rdu fil.
Indication : on utilisera le théorème de Gauss.
3.* En déduire le champ créé au point Msur le schéma ci-
contre, par un plan infini chargé σsur lequel il existe une
rayure très fine de largeur a, droite, et de longueur infinie.
M
4.* Montrer que la capacité du condensateur cylindrique ci-contre
s’écrit :
C=2πε0`
ln(b/a)
Indication : s’inspirer de la démonstration de la partie I sur le
condensateur sphérique terrestre.
z
la
b
2.2 Champs magnétique
1. On dispose deux fils parallèles infinis, parcourus par des cou-
rants I1et I2dans le même sens et séparés d’une distance
d. Calculer le champ magnétique entre les deux fils.
2.* On dispose d’une aiguille aimantée libre de tourner autour
de l’axe (Oz). Sous l’influence du champ magnétique ter-
restre, noté ~ BH, l’aiguille s’aligne avec ~ BH. Une fois l’équi-
libre atteint, on place une spire de telle sorte que le plan de
celle-ci contienne l’aiguille aimantée, comme indiqué sur le
schéma ci-contre. On fait ensuite circuler un courant I. Une
fois l’équilibre atteint, on remarque que l’aiguille aimantée
a tourné d’un angle θautour de l’axe (Oz). Exprimer le
champ magnétique terrestre ~ BHen fonction de cet angle θ,
du courant Iet du rayon Rde la spire.
x
y
z
I1I2
d
x
y
O
Devoir maison numéro 1 3 B Lamine, N Treps