Analyse de l`influence des inerties thermique et dynamique sur les

Analyse de l’influence des inerties thermique et
dynamique sur les conditions de d´ eclenchement de la
nucl´ eation
Laetitia LEAL1, Pascal LAVIEILLE1, Marc MISCEVIC1∗, Loun` es TADRIST2, Fr´ ed´ eric
TOPIN 2
1LAboratoire PLAsma et Conversion de l’Energie - LAPLACE - UMR 5213 - Universit´
e Paul Sabatier
118 route de Narbonne - 31062 Toulouse
2Laboratoire IUSTI - 5 rue Enrico Fermi - Technopˆ
ole de chˆ ateau Gombert
13453 Marseille Cedex 13
∗(auteur correspondant : marc.mise[email protected])
R´ esum´ e - L’apparition de la nucl´ eation par processus simultan´ ee de l’´ ebullition et la cavitation est
´
etudi´ ee ` a l’aide d’un dispositif exp´ erimental mettant en oeuvre une d´ eformation dynamique d’une paroi
de confinement. Une ´ etude de l’effet des diff´ erents param` etres de d´ eformation est effectu´ ee et montre
une forte diminution de la surchauffe n´ ecessaire au d´ eclenchement de la nucl´ eation. Un outil num´ erique
est par la suite r´ ealis´ e afin d’´ etudier la physique dominant le comportement d’un embryon lorsque ce
dernier est soumis a un flux de chaleur et lorsque la pression du liquide l’environnant impos´ ee oscille
au cours du temps.
Nomenclature
a0amplitude maximale, m
edistance entre la paroi chauffante et la
paroi de confinement au repos, m
ffr´ equence de la d´ eformation de la paroi
de confinement, Hz
Llongueur, m
ppression, P a
rrayon, m
ttemps, s
Ttemp´ erature, K
∆TON B surchauffe au d´ eclenchement, K
urvecteur unitaire
Indices
atm atmosph` ere
ccavit´ e
lliquide
l/v interface liquide/vapeur
max maximum
pparoi
ssolide
sat saturation
vvapeur
∞infini
1. Introduction
Les besoins en terme de transferts de chaleur sont en constante augmentation que ce soit
dans l’industrie conventionnelle ou dans l’industrie de pointe. Un des moyens prometteurs
pour r´ epondre ` a ces besoins d’intensification des transferts de chaleur est de mettre en oeuvre
le changement de phase [1]. Toutefois, un verrou technologique diminue la fiabilit´ e de ces
proc´ ed´ es. En effet, le niveau de temp´ erature n´ ecessaire ` a l’apparition de la nucl´ eation peut ˆ etre
cons´ equent ce qui peut engendrer l’endommagement, voire la destruction, du syst` eme. Pour
r´ esoudre ce probl` eme, une technique de contrˆ ole du d´ eclenchement de la nucl´ eation a ´ et´ e pro-
pos´ ee [2, 3]. Elle consiste ` a d´ eformer dynamiquement une paroi de confinement afin d’engen-
drer des oscillations de la pression du liquide au cours du temps. L’id´ ee avanc´ ee dans ce travail
consiste ` a combiner les effets d’un apport de chaleur et d’une diminution de pression afin de
contrˆ oler la temp´ erature de la paroi solide au moment o` u la nucl´ eation est amorc´ ee. On parle

alors d’effets combin´ es d’´ ebullition et de cavitation. Une premi` ere campagne exp´ erimentale a
montr´ e que cette technique ´ etait efficiente puisque la diminution de la surchauffe n´ ecessaire
au d´ eclenchement de la nucl´ eation est diminu´ ee de plus de 80% lorsque la d´ eformation dy-
namique de la paroi de confinement a lieu [3]. Pour mieux comprendre, cette forte diminu-
tion de la surchauffe ` a l’apparition de la nucl´ eation, une ´ etude des effets des diff´ erents pa-
ram` etres de la d´ eformation dynamique est pr´ esent´ ee. Les r´ esultats exp´ erimentaux ont ´ et´ e com-
par´ es aux r´ esultats th´ eoriques d’un mod` ele de nucl´ eation ”classique” [4] : de forts ´ ecarts sont
constat´ es entre les surchauffes au d´ eclenchement ´ evalu´ ees par la th´ eorie ”classique” de la
nucl´ eation et ceux obtenus exp´ erimentalement. Au cours de cette communication, une analyse
de la nucl´ eation par processus simultan´ es de l’´ ebullition et de la cavitation est propos´ ee.
2. Etude exp´ erimentale
L’obtention des effets combin´ es d’´ ebullition et de cavitation n´ ecessite de d´ evelopper un
syst` eme permettant d’apporter de la chaleur ` a une paroi et un syst` eme permettant de faire varier
de fac¸on dynamique la pression du liquide au contact de cette paroi. La configuration retenue [3]
consiste ` a confiner un liquide entre une paroi inf´ erieure chauff´ ee par une r´ esistance ´ electrique
et une paroi sup´ erieure pouvant ˆ etre d´ eform´ ee de fac¸on contrˆ ol´ ee en amplitude et en fr´ equence
grˆ ace ` a un actionneur pi´ ezo´ electrique. Cette d´ eformation implique des variations de quantit´ es
de mouvement du liquide et par voie de cons´ equence des oscillations de sa pression au cours du
temps.
Dans un premier temps, le d´ eclenchement de l’´ ebullition est ´ etudi´ ee lorsque l’actionneur
pi´ ezo´ electrique est ´ eteint. Pour ce faire, des ´ echelons de flux thermiques sont impos´ es ` a la pa-
roi chauff´ ee jusqu’` a ce que la temp´ erature de celle-ci atteigne une valeur suffisante pour que
l’´ ebullition soit amorc´ ee. La surchauffe au d´ eclenchement de l’´ ebullition est alors mesur´ ee.
Elle est d´ efinie par : ∆TON B =Tp,max −Tsat(patm). L’exp´ erience est r´ ep´ et´ ee quatre fois afin de
v´ erifier la reproductibilit´ e des r´ esultats et ceci pour diff´ erents degr´ es de confinement. Pour une
distance entre la paroi de confinement et la paroi chauff´ ee donn´ ee, l’amplitude maximale de la
dispersion entre les diff´ erents tests est de l’ordre de 3` a4˚C. Cette dispersion apparaˆ ıt tout ` a fait
acceptable compte-tenu du caract` ere stochastique de l’´ ebullition g´ en´ eralement report´ e dans la
litt´ erature. Les valeurs moyennes de la surchauffe pour les diff´ erents degr´ es de confinement se
situent entre 22,2et 23,5˚C. Ces r´ esultats obtenus mettent ´ egalement en ´ evidence que le degr´ e
de confinement ne joue pas un rˆ ole notable sur les conditions en temp´ erature que doit atteindre
la surface chauff´ ee pour que l’´ ebullition d´ emarre. Ainsi, pour toutes les valeurs de confine-
ment test´ ees (250 µm,500 µm et 2cm), en l’absence d’actionnement, la valeur de surchauffe
n´ ecessaire au d´ eclenchement de l’´ ebullition en vase est d’environ 23˚C.
La reproductibilit´ e des r´ esultats exp´ erimentaux ayant ´ et´ e v´ erifi´ ee et la surchauffe de d´ eclen-
chement de r´ ef´ erence ayant ´ et´ e d´ efinie, une ´ etude des effets des diff´ erents param` etres de d´ efor-
mation de la paroi de confinement sur les conditions de d´ eclenchement de la nucl´ eation est
effectu´ ee. Pour un ´ ecartement entre la paroi de confinement et la paroi chauff´ ee de 250 µm,
l’´ evolution de la surchauffe au d´ eclenchement de la nucl´ eation obtenue exp´ erimentalement en
fonction de l’amplitude de la d´ eformation dynamique ` a diff´ erentes fr´ equences est pr´ esent´ ee sur
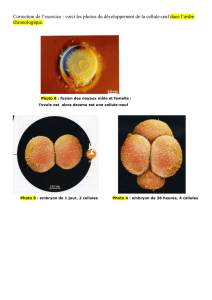
la figure 1. Pour les plus basses fr´ equences, les r´ esultats mettent en ´ evidence une d´ ecroissance
de ∆TON B lorsque l’amplitude augmente de 0` a60 µm pour une fr´ equence de 20 Hz et de 0
`
a120 µm pour une fr´ equence de 40 Hz, puis une stagnation de cette surchauffe. L’´ evolution

de la surchauffe au d´ eclenchement en fonction de la fr´ equence est similaire ` a celle en fonction
de l’amplitude. La surchauffe au d´ eclenchement diminue lorsque la fr´ equence augmente. Tou-
tefois, aux faibles amplitudes (a0= 60 µm et a0= 100 µm), augmenter la fr´ equence au-dessus
de 20 Hz n’engendre pas une diminution suppl´ ementaire de ∆TON B. Le degr´ e de confinement
a aussi une influence sur les conditions de d´ eclenchement lorsque la paroi de confinement est
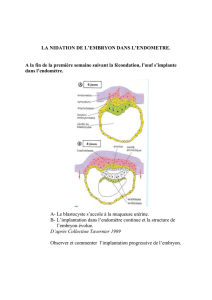
d´ eform´ ee dynamiquement. Les r´ esultats obtenus avec des ´ epaisseurs de l’espace confin´ e de 250
et 500 µm pour une amplitude de d´ eformation ´ egale ` a210 µm sont report´ es sur la figure 2.
Ils montrent que la diminution de la surchauffe au d´ eclenchement de la nucl´ eation est d’autant
moins significative que l’espacement entre les parois chauff´ ee et de confinement est important.
Or, sans d´ eformation dynamique de la paroi de confinement, la surchauffe au d´ eclenchement
est ind´ ependante du confinement : cette diff´ erence importante de comportement doit alors s’ex-
pliquer par des effets dynamiques li´ es ` a la d´ eformation de la paroi de confinement.
Cette ´ etude exp´ erimentale montre que la d´ eformation dynamique de la paroi de confinement
a un effet consid´ erable sur la condition en temp´ erature n´ ecessaire ` a l’apparition de la nucl´ eation.
En effet, la diminution maximale de la surchauffe au d´ eclenchement est importante (de l’ordre
de 86%).
0
5
10
15
20
25
0 30 60 90 120 150 180 210
ΔTONB (K)
Amplitude (µm)
f = 100 Hz
f= 60 Hz
f= 40 Hz
f= 20 Hz
Figure 1 : Evolution de ∆TON B en fonc-
tion de l’amplitude pour plusieurs fr´ equences
(e= 250 µm, n-pentane)
0
5
10
15
20
25
0 20 40 60 80 100 120
ΔTONB (K)
Fréquence (Hz)
e = 500 µm
e = 250 µm
Figure 2 : Evolution de ∆TON B en fonc-
tion de la fr´ equence pour plusieurs espacements
(a0= 210 µm, n-pentane)
A priori, en consid´ erant le mod` ele classique de nucl´ eation bas´ e sur la d´ estabilisation d’em-
bryons de vapeur pi´ eg´ es en paroi [4], cette diminution de la surchauffe n´ ecessaire au d´ eclen-
chement de la nucl´ eation est li´ ee ` a la baisse la pression du liquide au sein de l’espace confin´ e.
Pour quantifier l’oscillation de pression au cours du temps en fonction des param` etres de la
d´ eformation dynamique et du degr´ e de confinement, un mod` ele hydrodynamique a ´ et´ e d´ evelopp´ e
[5, 3]. Les r´ esultats exp´ erimentaux sont alors analys´ es en fonction du minimum de pression at-
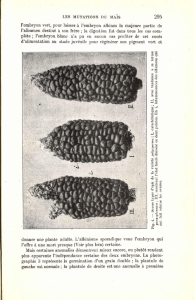
teint au cours du temps. La figure 3 repr´ esente l’´ evolution de la surchauffe au d´ eclenchement
de la nucl´ eation obtenue exp´ erimentalement et celle ´ evalu´ ee th´ eoriquement en fonction de la
d´ epression maximale atteinte au cours du temps . Lorsque la paroi de confinement n’est pas
d´ eform´ ee dynamiquement, la pression r´ egnant dans le liquide est constante au cours du temps
(nucl´ eation par processus d’´ ebullition). Une bonne coh´ erence est obtenue entre les surchauffes
au d´ eclenchement de la nucl´ eation ´ evalu´ ees th´ eoriquement et celles mesur´ ees exp´ erimentalement.

!"
#"
$!"
$#"
%!"
%#"
!&!'(!!" %&!'(!)" *&!'(!)" +&!'(!)" ,&!'(!)"
!"#$%&&'()&
!*+,-&'*.)&
-./-012-3456"
47-80-9:56"
'./;012-3456"
<7;801=>-"
+./&
Figure 3 : Comparaison des surchauffes au d´ eclenchement de la nucl´ eation th´ eoriques et exp´ erimentales
en fonction de la d´ epression maximale atteinte au cours du temps calcul´ ee par le mod` ele hydrodyna-
mique (rc= 0,2µm, n-pentane)
Par contre, lorsque la paroi de confinement est soumise ` a une d´ eformation dynamique (nucl´ eation
par processus de cavitation et d’´ ebullition), les surchauffes ` a l’apparition de la nucl´ eation ob-
tenues exp´ erimentalement sont tr` es diff´ erentes de celles ´ evalu´ ees th´ eoriquement. Ces ´ ecarts
traduisent a priori la non prise en compte dans le mod` ele classique (statique) de la nucl´ eation
de certains m´ ecanismes physiques qui vont dans le sens d’une favorisation de la nucl´ eation. Ces
m´ ecanismes sont donc a priori li´ es ` a des effets dynamiques.
Dans la partie suivante, une mod´ elisation d’un embryon pi´ eg´ e en paroi lorsqu’un flux de
chaleur lui est impos´ e et que la pression du liquide l’environnant oscille au cours du temps est
propos´ ee afin de comprendre la physique dominant le comportement de l’embryon.
3. Influence de la thermique et de l’inertie du liquide lors de la nucl´ eation
par processus simultan´ es de la cavitation et de l’´ ebullition
Diff´ erents effets dynamiques susceptibles d’expliquer cet ´ ecart entre la th´ eorie et l’exp´ erience
sont ´ etudi´ es. En conservant la th´ eorie de l’embryon pr´ eexistant accroch´ e` a une singularit´ e qui
apporte des r´ esultats satisfaisants dans le cas statique, la physique dominante de l’´ evolution de
l’embryon soumis ` a un flux thermique et dont la pression du liquide l’environnant oscille au
cours du temps est recherch´ ee. Ces deux ph´ enom` enes sont mod´ elis´ es pour tenter d’expliquer
leur influence simultan´ ee sur le d´ eclenchement de la nucl´ eation [6].
3.1. Description du mod` ele
Les acc´ el´ erations et d´ ec´ el´ erations du liquide au cours du temps sont impos´ ees ”loin” de l’em-
bryon puisqu’elles sont induites exp´ erimentalement par la d´ eformation dynamique de la paroi
de confinement. Or, ` a l’´ echelle de l’embryon (de l’ordre de 0,1µm) la vitesse du fluide ` a la
paroi due ` a la d´ eformation dynamique est quasi nulle, le fluide ´ etant suppos´ e Newtonien. Toute-
fois, l’oscillation de la pression du liquide au cours du temps et le changement d’´ etat induisent
des variations du volume de l’embryon : le rayon de courbure de l’interface liquide/vapeur est
modifi´ e ce qui engendre le mouvement du liquide ` a proximit´ e de l’embryon. Afin de r´ ealiser

liquide'
solide'
rc=rl/v''
r
u
&
r'
!"#$%&' #$()$%&'
!"#$%&'()*(
+,-*.$(
/-&'01.*23(
#*' #+'
,Ɛ͕ь'
,-'
,+͕ь'
,+./01' ,2'
4560$7156,15&'(().(258.5)*(*1().(6&25)*(9(
-,6(Ě͛ĞƐƉĂĐĞ()*(:;:<(="(
Figure 4 : Embryon de vapeur sph´ erique et d´ efinition du syst` eme de coordonn´ ees n´ ecessaires ` a la
mod´ elisation. Discr´ etisation des diff´ erents domaines d´ efinissant l’embryon.
un mod` ele 1D, seule cette direction principale de l’´ ecoulement est consid´ er´ ee. Ainsi quel que
soit le rayon de courbure de l’interface, seule la vitesse moyenne du liquide dans la direction
ur(figure 4) induite par les variations du volume de l’embryon et le changement d’´ etat sera
´
evalu´ ee. Par ailleurs, puisque la vitesse du liquide varie ` a proximit´ e de l’embryon, la pression
du liquide impos´ ee ”loin” de l’embryon et celle ` a son voisinage peuvent ˆ etre diff´ erentes. L’effet
de l’inertie du liquide est prise en compte dans cette mod´ elisation afin de capter ce ph´ enom` ene.
Pour mod´ eliser les couplages thermiques entre le liquide, la vapeur et l’interface, la diffusion
et le transport de la chaleur dans le liquide et dans le solide sont ´ egalement pris en compte. Les
´
equilibres thermodynamique et m´ ecanique de l’interface sont suppos´ es s’´ etablir instantan´ ement.
Pour disposer d’une mod´ elisation simplifi´ ee monodimensionnelle, seule la direction radiale est
consid´ er´ ee. Par ailleurs, les temps de diffusion de la chaleur dans la vapeur (de l’ordre de la
nanoseconde) sont tr` es faibles devant le temps caract´ eristique de l’oscillation de la pression au
cours du temps (0,01 s) et ceux de diffusion de la chaleur dans le liquide et dans le solide. Ceci
permet de consid´ erer la vapeur (et ses interfaces) comme un corps homog` ene en temp´ erature
(et en pression) mˆ eme si des flux de chaleur peuvent la traverser conform´ ement aux hypoth` eses
du corps mince thermiquement.
Par ailleurs, il est suppos´ e que le liquide est incompressible et que la vapeur se comporte comme
un gaz parfait. L’´ energie potentielle de pesanteur est n´ eglig´ ee puisque l’´ echelle de mod´ elisation
est de l’ordre du microm` etre.
Le mod` ele permet d’envisager des configurations en pr´ esence d’un flux de chaleur s’´ etablissant
entre la paroi et le liquide mais ´ egalement des configurations adiabatiques o` u la temp´ erature
dans le solide loin de l’embryon est impos´ ee ´ egale ` a la mˆ eme valeur que la temp´ erature du
fluide (´ egalement loin de l’embryon).
La mod´ elisation n´ ecessite (d’un point de vue num´ erique) la discr´ etisation des diff´ erents do-
maines du syst` eme. La figure 4 propose une vision sch´ ematique du syst` eme mod´ elis´ e. De part et
d’autre de l’embryon se situent le domaine solide et le domaine liquide. L’embryon est petit de-
vant ces deux domaines et est alors suppos´ e ponctuel. Le domaine liquide et le domaine solide
sont quant ` a eux discr´ etis´ es. En effet, il est n´ ecessaire de suivre l’´ evolution spatiale de la vitesse
(liquide), de la pression (liquide) et de la temp´ erature afin de quantifier l’inertie du liquide et les
flux thermiques (en prenant en compte les ph´ enom` enes de diffusion et de transport). Le syst` eme
d’´ equations implicite est resolu num´ eriquement.